
题目列表(包括答案和解析)
已知二次函数![]() 的二次项系数为
的二次项系数为![]() ,且不等式
,且不等式![]() 的解集为(1,3).
的解集为(1,3).
(1)若方程![]() 有两个相等的根,求
有两个相等的根,求![]() 的解析式;
的解析式;
(2)若函数![]() 的最大值不小于8,求实数
的最大值不小于8,求实数![]() 的取值范围。
的取值范围。
已知二次函数 的二次项系数为
的二次项系数为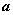 ,且不等式
,且不等式 的解集为(1,3).
的解集为(1,3).
(1)若方程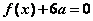 有两个相等的根,求
有两个相等的根,求 的解析式;
的解析式;
(2)若函数 的最大值不小于8,求实数
的最大值不小于8,求实数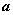 的取值范围。
的取值范围。
已知函数![]() 的最大值不大于
的最大值不大于![]() ,又当
,又当![]() ,求
,求![]() 的值。
的值。
某公司为了实现2011年1000万元的利润的目标,准备制定一个激励销售人员的奖励方案:销售利润达到10万元时,按销售利润进行奖励,且奖金数额y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金数额不超过5万元,同时奖金数额不超过利润的25%,现有二个奖励模型: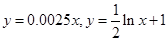 ,问其中是否有模型能完全符合公司的要求?说明理由。(解题提示:公司要求的模型只需满足:当
,问其中是否有模型能完全符合公司的要求?说明理由。(解题提示:公司要求的模型只需满足:当 时,①函数为增函数;②函数的最大值不超过5;③
时,①函数为增函数;②函数的最大值不超过5;③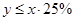 ,参考数据:
,参考数据: )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com