
题目列表(包括答案和解析)
若某产品的直径长与标准值的差的绝对值不超过1mm 时,则视为合格品,否则视为不合格品。在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品。计算这50件不合格品的直径长与标准值的差(单位:mm), 将所得数据分组,得到如下频率分布表:
|
分组 |
频数 |
频率 |
|
[-3, -2) |
|
0.10 |
|
[-2, -1) |
8 |
|
|
(1,2] |
|
0.50 |
|
(2,3] |
10 |
|
|
(3,4] |
|
|
|
合计 |
50 |
1.00 |
(Ⅰ)将上面表格中缺少的数据填在答题卡的相应位置;
(Ⅱ)估计该厂生产的此种产品中,不合格品的直径长与标准值的差落在区间(1,3]内的概率;
(Ⅲ)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品。据此估算这批产品中的合格品的件数。
【解析】(Ⅰ)
|
分组 |
频数 |
频率 |
|
[-3, -2) |
5 |
0.10 |
|
[-2, -1) |
8 |
0.16 |
|
(1,2] |
25 |
0.50 |
|
(2,3] |
10 |
0.2 |
|
(3,4] |
2 |
0.04 |
|
合计 |
50 |
1.00 |
(Ⅱ)根据频率分布表可知,落在区间(1,3]内频数为35,故所求概率为0.7.
(Ⅲ)由题可知不合格的概率为 0.01,故可求得这批产品总共有2000,故合格的产品有1980件。
0.01,故可求得这批产品总共有2000,故合格的产品有1980件。
 12、为了考察某种大麦穗长的分布情况,在一块试验地里抽取了100个穗,量得它们的长度(单位:cm)之后,将所得数据以0.3cm为组距,分成如下12个组:3.95~4.25,4.25~4.55,4.55~4.85,…,6.95~7.25,7.25~7.55,通过分析计算,最后画出的频数分布直方图如图,由图可知( )
12、为了考察某种大麦穗长的分布情况,在一块试验地里抽取了100个穗,量得它们的长度(单位:cm)之后,将所得数据以0.3cm为组距,分成如下12个组:3.95~4.25,4.25~4.55,4.55~4.85,…,6.95~7.25,7.25~7.55,通过分析计算,最后画出的频数分布直方图如图,由图可知( )设椭圆  :
: (
( )的一个顶点为
)的一个顶点为 ,
,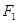 ,
, 分别是椭圆的左、右焦点,离心率
分别是椭圆的左、右焦点,离心率
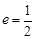 ,过椭圆右焦点
,过椭圆右焦点
 的直线
的直线 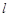 与椭圆
与椭圆 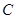 交于
交于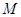 ,
,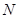 两点.
两点.
(1)求椭圆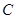 的方程;
的方程;
(2)是否存在直线 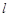 ,使得
,使得
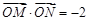 ,若存在,求出直线
,若存在,求出直线
 的方程;若不存在,说明理由;
的方程;若不存在,说明理由;
【解析】本试题主要考查了椭圆的方程的求解,以及直线与椭圆的位置关系的运用。(1)中椭圆的顶点为 ,即
,即 又因为
又因为 ,得到
,得到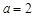 ,然后求解得到椭圆方程(2)中,对直线分为两种情况讨论,当直线斜率存在时,当直线斜率不存在时,联立方程组,结合
,然后求解得到椭圆方程(2)中,对直线分为两种情况讨论,当直线斜率存在时,当直线斜率不存在时,联立方程组,结合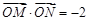 得到结论。
得到结论。
解:(1)椭圆的顶点为 ,即
,即
 ,解得
,解得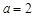 ,
,
 椭圆的标准方程为
椭圆的标准方程为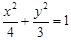 --------4分
--------4分
(2)由题可知,直线 与椭圆必相交.
与椭圆必相交.
①当直线斜率不存在时,经检验不合题意. --------5分
②当直线斜率存在时,设存在直线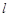 为
为 ,且
,且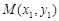 ,
, .
.
由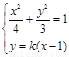 得
得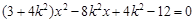 , ----------7分
, ----------7分
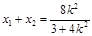 ,
, ,
,
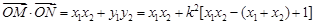
=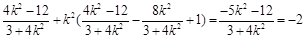
所以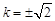 ,
----------10分
,
----------10分
故直线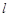 的方程为
的方程为 或
或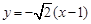
即 或
或
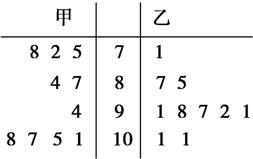 7、如图是甲、乙两名射击运动员各射击10次后所得到的成绩的茎叶图(茎表示成绩的整数环数,叶表示小数点后的数字),由图可知( )
7、如图是甲、乙两名射击运动员各射击10次后所得到的成绩的茎叶图(茎表示成绩的整数环数,叶表示小数点后的数字),由图可知( )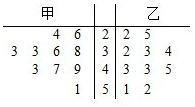
| A、甲、乙两队得分的平均数相等 | B、甲、乙两队得分的中位数相等 | C、甲、乙两队得分的极差相等 | D、甲、乙两队得分在[30,39)分数段的频率相等 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com