
题目列表(包括答案和解析)
已知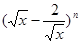 二项展开式中,第4项的二项式系数与第3项的二项式系数的比为8:3.(I)求n的值;(II)求展开式中
二项展开式中,第4项的二项式系数与第3项的二项式系数的比为8:3.(I)求n的值;(II)求展开式中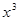 项的系数.
项的系数.
【解析】本试题主要是考查了二项式定理的运用,求解通项公式的项的运用。
设二项式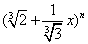
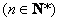 的展开式中第7项的系数与倒数第7项的系数之比是
的展开式中第7项的系数与倒数第7项的系数之比是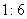 .
.
(Ⅰ)求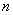 ;
;
(Ⅱ)展开式中有多少项的系数是有理数,指出它们分别是哪几项.
本题考查二项式定理、二项式系数与系数的概念、二项式定理的通项的应用,属基本题
设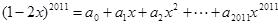 ,求下列各式的值:
,求下列各式的值:
(Ⅰ)  ;
(Ⅱ)
;
(Ⅱ) ; (Ⅲ)
; (Ⅲ) .
.
【解析】本试题主要考查了二项式定理的运用。第一问中利用赋值的思想,令x=0,得到
第二问中,利用令x=1,得到
第三问中,利用令x=1/2,得到
解:(1)令x=0,得到 ;
;
(2)令x=1,得到

(3)令x=1/2,得到

已知 ,且
,且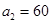 .
.
(1)求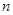 的值;
的值;
(2)求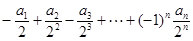 的值.
的值.
【解析】本试题主要考查了二项式定理的运用,以及系数求和的赋值思想的运用。第一问中,因为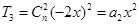 ,所以
,所以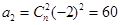 ,可得
,可得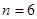 ,第二问中,因为
,第二问中,因为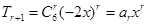 ,所以
,所以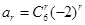 ,所以
,所以 ,利用组合数性质可知。
,利用组合数性质可知。
解:(1)因为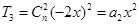 ,所以
,所以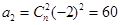 , ……3分
, ……3分
化简可得 ,且
,且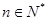 ,解得
,解得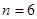 . …………6分
. …………6分
(2)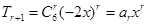 ,所以
,所以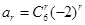 ,
,
所以 ,
,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com