
题目列表(包括答案和解析)
我们知道,二次函数y=ax2+bx+c(a≠0)的图象是一条抛物线,那么这条抛物线的顶点坐标、焦点坐标、准线方程如何确定?
探究:对于二次函数的解析式进行配方,注意观察与抛物线的标准方程形式对比,可以发现其方程形式与标准方程中的一种形式有些相似,借助于图象的平移不难得到其顶点坐标、焦点坐标和准线方程.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
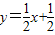 与抛物线交于点E.问:在抛物线的对称轴上是否存在这样的点F,使得△ABE与以B、D、F为顶点的三角形相似,若存在,求出点F的坐标;若不存在,请说明理由;
与抛物线交于点E.问:在抛物线的对称轴上是否存在这样的点F,使得△ABE与以B、D、F为顶点的三角形相似,若存在,求出点F的坐标;若不存在,请说明理由;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com