
题目列表(包括答案和解析)
已知函数 (
( 为实数).
为实数).
(Ⅰ)当 时,求
时,求 的最小值;
的最小值;
(Ⅱ)若 在
在 上是单调函数,求
上是单调函数,求 的取值范围.
的取值范围.
【解析】第一问中由题意可知: . ∵
. ∵ ∴
∴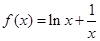 ∴
∴
 .
.
当 时,
时, ;
当
;
当 时,
时, . 故
. 故 .
.
第二问
 .
.
当 时,
时, ,在
,在 上有
上有 ,
, 递增,符合题意;
递增,符合题意;
令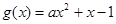 ,则
,则
 ,∴
,∴ 或
或 在
在 上恒成立.转化后解决最值即可。
上恒成立.转化后解决最值即可。
解:(Ⅰ) 由题意可知: . ∵
. ∵ ∴
∴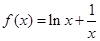 ∴
∴
 .
.
当 时,
时, ;
当
;
当 时,
时, . 故
. 故 .
.
(Ⅱ) 
 .
.
当 时,
时, ,在
,在 上有
上有 ,
, 递增,符合题意;
递增,符合题意;
令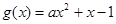 ,则
,则
 ,∴
,∴ 或
或 在
在 上恒成立.∵二次函数
上恒成立.∵二次函数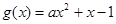 的对称轴为
的对称轴为 ,且
,且
∴ 或
或
 或
或
 或
或
 或
或 . 综上
. 综上
如图是甲、乙两名射击运动员各射击10次后所得到的成绩的茎叶图(茎表示成绩的整数环数,叶表示小数点后的数字),由图可知( )
A.甲、乙中位数的和为18.2,乙稳定性高B.甲、乙中位数的和为17.8,甲稳定性高
C.甲、乙中位数的和为18.5,甲稳定性高D.甲、乙中位数的和为18.65,乙稳定性高

汕头二中拟建一座长 米,宽
米,宽 米的长方形体育馆.按照建筑要求,每隔
米的长方形体育馆.按照建筑要求,每隔 米(
米( ,
, 为正常数)需打建一个桩位,每个桩位需花费
为正常数)需打建一个桩位,每个桩位需花费 万元(桩位视为一点且打在长方形的边上),桩位之间的
万元(桩位视为一点且打在长方形的边上),桩位之间的 米墙面需花
米墙面需花 万元,在不计地板和天花板的情况下,当
万元,在不计地板和天花板的情况下,当 为何值时,所需总费用最少?
为何值时,所需总费用最少?
【解析】本试题主要考查了导数在研究函数中的运用。先求需打 个桩位.再求解墙面所需费用为:
个桩位.再求解墙面所需费用为: ,最后表示总费用
,最后表示总费用 ,利用导数判定单调性,求解最值。
,利用导数判定单调性,求解最值。
解:由题意可知,需打 个桩位.
…………………2分
个桩位.
…………………2分
墙面所需费用为: ,……4分
,……4分
∴所需总费用
 (
( )…7分
)…7分
令 ,则
,则
当 时,
时, ;当
;当 时,
时, .
.
∴当 时,
时,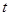 取极小值为
取极小值为 .而在
.而在 内极值点唯一,所以
内极值点唯一,所以 .∴当
.∴当 时,
时, (万元),即每隔3米打建一个桩位时,所需总费用最小为1170万元.
(万元),即每隔3米打建一个桩位时,所需总费用最小为1170万元.
为了考查某种大麦穗长的分布情况,在一块试验地里抽取了100个穗,量得它们的长度(单位:cm)之后,将所得数据以0.3 cm为组距,分成如下12个组:3.95~4.25,4.25~4.55,4.55~4.85,…,6.95~7.25,7.25~7.55,通过分析计算,最后画出频率分布直方图如下图:

由图可知
A.长度在5.45~5.75 cm范围内的麦穗所占的比最大
B.长度在5.15~5.45 cm范围内的麦穗所占的比大于255
C.长度在5.75~6.05 cm范围内的麦穗的比最大
D.长度在5.45~5.75 cm范围内的麦穗比长度在6.35~6.65 cm范围内的麦穗少
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com