
题目列表(包括答案和解析)
椭圆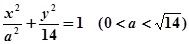 的两焦点为
的两焦点为 ,现将坐标平面沿
,现将坐标平面沿 轴折成二面角,二面角的度数为
轴折成二面角,二面角的度数为 ,已知折起后两焦点的距离
,已知折起后两焦点的距离 ,则满足题设的一组数值:
,则满足题设的一组数值:
 (只需写出一组就可以,不必写出所有情况)
(只需写出一组就可以,不必写出所有情况)
解:(Ⅰ)设![]() :
:![]()
![]() ,其半焦距为
,其半焦距为![]()
![]() .则
.则![]() :
:![]() .
.
由条件知![]() ,得
,得![]() .
.
![]() 的右准线方程为
的右准线方程为![]() ,即
,即![]() .
.
![]() 的准线方程为
的准线方程为![]() .
.
由条件知![]() , 所以
, 所以![]() ,故
,故![]() ,
,![]() .
.
从而![]() :
:![]() ,
, ![]() :
:![]() .
.
(Ⅱ)由题设知![]() :
:![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() .
.
由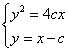 ,得
,得![]() ,所以
,所以![]() .
.
而![]() ,由条件
,由条件![]() ,得
,得![]() .
.
由(Ⅰ)得![]() ,
,![]() .从而,
.从而,![]() :
:![]() ,即
,即![]() .
.
由 ,得
,得![]() .所以
.所以![]() ,
,![]() .
.
故![]() .
.
设椭圆 (常数
(常数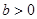 )的左右焦点分别为
)的左右焦点分别为 ,
, 是直线
是直线 上的两个动点,
上的两个动点, .
.
(1)若 ,求
,求 的值;
的值;
(2)求 的最小值.
的最小值.

【解析】第一问中解:设 ,
, 则
则
由 得
得 由
由 ,得
,得
 ②
②

第二问易求椭圆 的标准方程为:
的标准方程为:
 ,
,
所以,当且仅当 或
或 时,
时, 取最小值
取最小值 .
.
解:设 ,
, ……………………1分
……………………1分
则 ,由
,由 得
得 ①……2分
①……2分
(1)由 ,得
,得 ② ……………1分
② ……………1分
 ③ ………………………1分
③ ………………………1分
由①、②、③三式,消去 ,并求得
,并求得 .
………………………3分
.
………………………3分
(2)解法一:易求椭圆 的标准方程为:
的标准方程为: .………………2分
.………………2分
 , ……4分
, ……4分
所以,当且仅当 或
或 时,
时, 取最小值
取最小值 .…2分
.…2分
解法二: ,
………………4分
,
………………4分
所以,当且仅当 或
或 时,
时, 取最小值
取最小值
如图,三棱柱 中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。
中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。

(I) 证明:平面 ⊥平面
⊥平面
(Ⅱ)平面 分此棱柱为两部分,求这两部分体积的比.
分此棱柱为两部分,求这两部分体积的比.
【命题意图】本题主要考查空间线线、线面、面面垂直的判定与性质及几何体的体积计算,考查空间想象能力、逻辑推理能力,是简单题.
【解析】(Ⅰ)由题设知BC⊥ ,BC⊥AC,
,BC⊥AC, ,∴
,∴ 面
面 , 又∵
, 又∵
 面
面 ,∴
,∴ ,
,
由题设知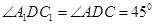 ,∴
,∴ =
= ,即
,即 ,
,
又∵ , ∴
, ∴ ⊥面
⊥面 , ∵
, ∵
 面
面 ,
,
∴面 ⊥面
⊥面 ;
;
(Ⅱ)设棱锥 的体积为
的体积为 ,
, =1,由题意得,
=1,由题意得, =
= =
= ,
,
由三棱柱 的体积
的体积 =1,
=1,
∴ =1:1, ∴平面
=1:1, ∴平面 分此棱柱为两部分体积之比为1:1
分此棱柱为两部分体积之比为1:1
已知 ,设
,设 ,则由函数
,则由函数 的图象与x轴、直线
的图象与x轴、直线 所围成的封闭图形的面积为 .
所围成的封闭图形的面积为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com