如图，平面ABDE⊥平面ABC，ACBC，AC=BC=4，四边形ABDE是直角梯形，BDAE，BDBA，AE=2BD=4，O、M分别为CE、AB的中点.

（Ⅰ）证明：OD//平面ABC；

（Ⅱ）能否在EM上找一点N，使得ON⊥平面ABDE？若能，请指出点N的位置，并加以证明；若不能，请说明理由.

【解析】第一问：取AC中点F，连结OF、FB.∵F是AC的中点，O为CE的中点，

∴OF∥EA且OF=且BD=

∴OF∥DB，OF=DB，

∴四边形BDOF是平行四边形。

∴OD∥FB

第二问中，当N是EM中点时，ON⊥平面ABDE。           ………7分

证明：取EM中点N，连结ON、CM， AC=BC，M为AB中点，∴CM⊥AB，

又∵面ABDE⊥面ABC，面ABDE面ABC=AB，CM面ABC，

∴CM⊥面ABDE，∵N是EM中点，O为CE中点，∴ON∥CM，

∴ON⊥平面ABDE。

 

已知正方形ABCD的边长为1，分别取边BC、CD的中点E、F，连结AE、EF、AF，以AE、EF、FA为折痕，折叠使点B、C、D重合于一点P.

(1)求证：AP⊥EF；

(2)求证：平面APE⊥平面APF；

(3)求异面直线PA和EF的距离.

已知离心率为的椭圆的中心在原点，焦点在x轴上，双曲线以椭圆的长轴为实轴，短轴为虚轴，且焦距为2．
（I）求椭圆及双曲线的方程；
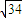（Ⅱ）设椭圆的左、右顶点分别为A，B，在第二象限内取双曲线上一点P，连结BP交椭圆于点M，连结PA并延长交椭圆于点N，若=．求四边形ANBM的面积．

 

    （理）如图2，E、F分别是矩形ABCD的边AB、CD的中点，G是EF上的一点.

将△GAB、△GCB分别沿AB、CD翻折成△G₁AB、△G₂CD，并连结G₁G₂，使得平面G₁AB⊥平面ABCD，G₁G₂//AD，且G₁G₂<AD. 连结BG₂，如图3.

   （Ⅰ）证明平面G₁AB⊥平面G₁ADG₂；

   （Ⅱ）当AB=12，BC=25，EG=8时，求直线BG₂和平面G₁ADG₂所成的角.

 

 

 

（文）已知某质点的运动方程为，其运动轨迹的一部分如图所示.

   （1）试确定b、c的值；

   （2）若当恒成立，

求d的取值范围.