
题目列表(包括答案和解析)
 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB=| π | 6 |
 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB=| π | 6 |
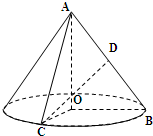 (2009•普陀区一模)如图,在 Rt△AOB中,∠OAB=
(2009•普陀区一模)如图,在 Rt△AOB中,∠OAB=| π | 6 |
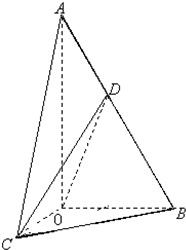 如图,在Rt△AOB中,∠OAB=30°,斜边AB=4.Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角.动点D在斜边AB上.
如图,在Rt△AOB中,∠OAB=30°,斜边AB=4.Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角.动点D在斜边AB上.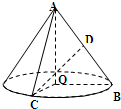 如图,在 Rt△AOB中,∠OAB=
如图,在 Rt△AOB中,∠OAB=| π | 6 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com