
题目列表(包括答案和解析)
A.任意三个元素 B.两边和一个角 C.一边和两个角 D.三边
在三角形的六个元素中,已知下列哪一组条件,一定可以利用余弦定理来解三角形,这一组是( )
A.任意三个元素 B.两边和一个角 C.一边和两个角 D.三边
已知△ 中,A,B,C。的对边分别为a,b,c,且
中,A,B,C。的对边分别为a,b,c,且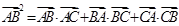
(1)判断△ 的形状,并求sinA+sinB的取值范围。
的形状,并求sinA+sinB的取值范围。
(2)若不等式 ,对任意的满足题意的a,b,c都成立,求实数k的取值范围.
,对任意的满足题意的a,b,c都成立,求实数k的取值范围.
【解析】第一问利用余弦定理和向量的数量积公式得到

判定形状,并且求解得到sinA+sinB的取值范围
第二问中,对于不等式恒成立问题,分离参数法,得到结论。
在△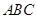 中,∠
中,∠ ,∠
,∠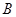 ,∠
,∠ 的对边分别是
的对边分别是 ,且
,且
 .
.
(1)求∠ 的大小;(2)若
的大小;(2)若 ,
, ,求
,求 和
和 的值.
的值.
【解析】第一问利用余弦定理得到
 第二问
第二问
(2) 由条件可得 
将  代入 得 bc=2
代入 得 bc=2
解得 b=1,c=2 或 b=2,c=1 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com