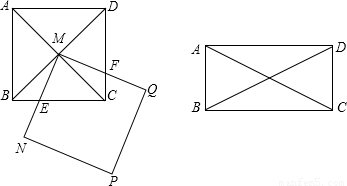
(2012•南关区模拟)如图,在梯形ABCD中,AB∥CD,AD⊥AB,AD=8cm,DC=8cm,AB=12cm.点P从点A出发,沿线段AD匀速运动,与此同时,点Q从点B出发,沿线段BA匀速运动,P、Q两点运动的速度均为1cm/s,当其中一点到达终点时,另一点也停止运动,过点Q作QM⊥AB交折线BC-CD于点M.以线段MQ为直角边在MQ的左侧作等腰直角△MQN,以线段AP为一边在AP的右侧作正方形APEF,设运动时间为t(s),△MQN与正方形APEF重叠部分的面积为S(cm).

(1)求两点N、F相遇时t的值;
(2)求S与t的函数关系式;
(3)当点M在线段CD上运动时,设MN分别交PE、PA于点G、H,请直接写出在此时段△PGH扫过平面部分的面积.