
题目列表(包括答案和解析)
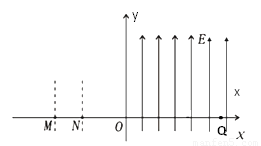
 如图所示,直角坐标系的ox轴水平,oy轴竖直;M点坐标为(-0.3m,0)、N点坐标为(-0.2m,0);在-0.3m≤X≤-0.2m的长条形范围内存在竖直方向的匀强电场E0;在X≥0的范围内存在竖直向上的匀强电场,场强为E=20N/C;在第一象限的某处有一圆形的匀强磁场区,磁场方向垂直纸面向外,磁感应强度B=2.5T.有一带电量q=+1.0×10-4C、质量m=2×10-4kg的微粒以v0=0.5m/s的速度从M点沿着x轴正方向飞入电场,恰好垂直经过y轴上的P点(图中未画出,yP>0),而后微粒经过第一象限某处的圆形磁场区,击中x轴上的Q点,速度方向与x轴正方向夹角为60°.g取10m/s2.求:
如图所示,直角坐标系的ox轴水平,oy轴竖直;M点坐标为(-0.3m,0)、N点坐标为(-0.2m,0);在-0.3m≤X≤-0.2m的长条形范围内存在竖直方向的匀强电场E0;在X≥0的范围内存在竖直向上的匀强电场,场强为E=20N/C;在第一象限的某处有一圆形的匀强磁场区,磁场方向垂直纸面向外,磁感应强度B=2.5T.有一带电量q=+1.0×10-4C、质量m=2×10-4kg的微粒以v0=0.5m/s的速度从M点沿着x轴正方向飞入电场,恰好垂直经过y轴上的P点(图中未画出,yP>0),而后微粒经过第一象限某处的圆形磁场区,击中x轴上的Q点,速度方向与x轴正方向夹角为60°.g取10m/s2.求:如图所示,直角坐标系的ox轴水平,oy轴竖直;M点坐标为(-0.3m,0)、N点坐标为(-0.2m,0);在 -0.3m ≤ X ≤ -0.2m的长条形范围内存在竖直方向的匀强电场E0;在X ≥0的范围内存在竖直向上的匀强电场,场强为E=20N/C;在第一象限的某处有一圆形的匀强磁场区,磁场方向垂直纸面向外,磁感应强度B=2.5T。有一带电量q =+1.0×10-4C、质量m=2×10-4kg的微粒以v0=0.5m/s的速度从M点沿着x轴正方向飞入电场,恰好垂直经过y轴上的P点(图中未画出, yP>0),而后微粒经过第一象限某处的圆形磁场区,击中x轴上的Q点,速度方向与x轴正方向夹角为600。g取10m/s2。求:
1.场强E0的大小和方向;
2.P点的坐标及圆形磁场区的最小半径r;
3.微粒从进入最小圆形磁场区到击中Q点的运动时间(可以用根号及π等表示)
如图所示,直角坐标系的ox轴水平,oy轴竖直;M点坐标为(-0.3m,0)、N点坐标为(-0.2m,0);在 -0.3m ≤ X ≤ -0.2m的长条形范围内存在竖直方向的匀强电场E0;在X ≥0的范围内存在竖直向上的匀强电场,场强为E=20N/C;在第一象限的某处有一圆形的匀强磁场区,磁场方向垂直纸面向外,磁感应强度B=2.5T。有一带电量q =+1.0×10-4C、质量m=2×10-4kg的微粒以v0=0.5m/s的速度从M点沿着x轴正方向飞入电场,恰好垂直经过y轴上的P点(图中未画出, yP>0),而后微粒经过第一象限某处的圆形磁场区,击中x轴上的Q点,速度方向与x轴正方向夹角为600。g取10m/s2。求:
1.场强E0的大小和方向;
2.P点的坐标及圆形磁场区的最小半径r;
3.微粒从进入最小圆形磁场区到击中Q点的运动时间(可以用根号及π等表示)
如图所示,直角坐标系的ox轴水平,oy轴竖直;M点坐标为(-0.3m,0)、N点坐标为(-0.2m,0);在 -0.3m ≤ X ≤ -0.2m的长条形范围内存在竖直方向的匀强电场E0;在X ≥0的范围内存在竖直向上的匀强电场,场强为E=20N/C;在第一象限的某处有一圆形的匀强磁场区,磁场方向垂直纸面向外,磁感应强度B=2.5T。有一带电量q =+1.0×10-4C、质量m=2×10-4kg的微粒以v0=0.5m/s的速度从M点沿着x轴正方向飞入电场,恰好垂直经过y轴上的P点(图中未画出,yP>0),而后微粒经过第一象限某处的圆形磁场区,击中x轴上的Q点,速度方向与x轴正方向夹角为600。g取10m/s2。求:
1.场强E0的大小和方向;
2.P点的坐标及圆形磁场区的最小半径r;
3.微粒从进入最小圆形磁场区到击中Q点的运动时间(可以用根号及π等表示)
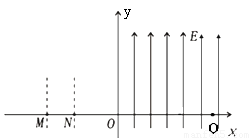
如图所示,直角坐标系的ox轴水平,oy轴竖直;M点坐标为(-0.3m,0)、N点坐标为(-0.2m,0);在 -0.3m ≤ X ≤ -0.2m的长条形范围内存在竖直方向的匀强电场E0;在X ≥0的范围内存在竖直向上的匀强电场,场强为E=20N/C;在第一象限的某处有一圆形的匀强磁场区,磁场方向垂直纸面向外,磁感应强度B=2.5T。有一带电量q =+1.0×10-4C、质量m=2×10-4kg的微粒以v0=0.5m/s的速度从M点沿着x轴正方向飞入电场,恰好垂直经过y轴上的P点(图中未画出, yP>0),而后微粒经过第一象限某处的圆形磁场区,击中x轴上的Q点,速度方向与x轴正方向夹角为600。g取10m/s2。求:
1.场强E0的大小和方向;
2.P点的坐标及圆形磁场区的最小半径r;
3.微粒从进入最小圆形磁场区到击中Q点的运动时间(可以用根号及π等表示)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com