
题目列表(包括答案和解析)
| 3 |
宇航员在一星球表面上的某高处,沿水平方向抛出一小球。经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L。若抛出时初速度增大到2倍,则抛出点与落地点之间的距离为![]() L。已知两落地点在同一水平面上,该星球的半径为R,万有引力常数为G。求该星球的质量M。
L。已知两落地点在同一水平面上,该星球的半径为R,万有引力常数为G。求该星球的质量M。
(10分)宇航员在一星球表面上的某高处,沿水平方向抛出一个小球,经时间t,小球落到星球表面,测出抛出点与落地点之间距离为L。若抛出时的初速增大到原来的2倍,则抛出点到落地点间的距离为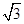 L。已知两落地点在同一水平面上,该星球的质量M,万有引力常数为G,求:
L。已知两落地点在同一水平面上,该星球的质量M,万有引力常数为G,求:
(1)该星球的半径R。
(2)该星球上的第一宇宙速度。
(10分)宇航员在一星球表面上的某高处,沿水平方向抛出一个小球,经时间t,小球落到星球表面,测出抛出点与落地点之间距离为L。若抛出时的初速增大到原来的2倍,则抛出点到落地点间的距离为 L。已知两落地点在同一水平面上,该星球的质量M,万有引力常数为G,求:
L。已知两落地点在同一水平面上,该星球的质量M,万有引力常数为G,求:
(1)该星球的半径R。
(2)该星球上的第一宇宙速度。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com