
题目列表(包括答案和解析)
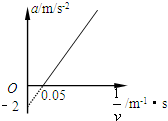 (2011?河东区一模)(1)一辆汽车在平直的公路上以某一初速度运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数(1/v)图象如图所示.若已知汽车的质量为m=1.5×103kg,则汽车运行时的功率为
(2011?河东区一模)(1)一辆汽车在平直的公路上以某一初速度运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数(1/v)图象如图所示.若已知汽车的质量为m=1.5×103kg,则汽车运行时的功率为| ×10 | 3 |
| ×10 | 3 |
| ||||||||||||
| 2x |
| ||||||||||||
| 2x |
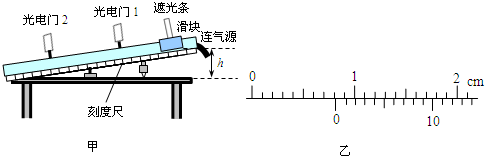
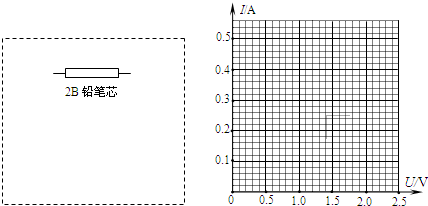
| U/V | 0.00 | 0.40 | 0.80 | 1.20 | 1.60 | 2.00 |
| I/A | 0.00 | 0.10 | 0.18 | 0.28 | 0.38 | 0.48 |

| A | 1-A |
(2013·上海模拟)如图10甲所示,在水平路段AB上有一质量为2×103 kg的汽车,正以10 m/s的速度向右匀速运动,汽车前方的水平路段BC较粗糙,汽车通过整个ABC路段的v-t图象如图乙所示(在t=15 s处水平虚线与曲线相切),运动过程中汽车发动机的输出功率保持20 kW不变,假设汽车在两个路段上受到的阻力(含地面摩擦力和空气阻力等)各自有恒定的大小。
(1)求汽车在AB路段上运动时所受的阻力Ff1。
(2)求汽车刚好到达B点时的加速度a。
(3)求BC路段的长度。

图10

 ;)
;)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com