
题目列表(包括答案和解析)
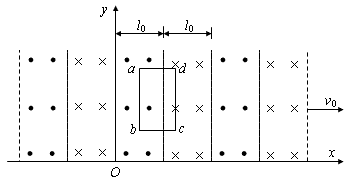
如图所示,在平面直角坐标系xOy第一象限内分布有垂直xOy向外的匀强磁场,磁感应强度大小B=2.5×10-2 T.在第二象限紧贴y轴并垂直y轴放置一对平行金属板MN,极板间距d=0.4 m,MN中心轴线离x轴0.3 m.极板与左侧电路相连接,通过移动滑动头P可以改变极板MN间的电压。a、b为滑动变阻器的最下端和最上端(滑动变阻器的阻值分布均匀),a、b两端所加电压U=1×102 V。在MN中心轴线上距y轴距离为L=0.4 m处,有一粒子源S沿x轴正方向连续射出比荷为 =4.0×106 C/kg,速度为v0=2.0×104 m/s带正电的粒子,粒子经过y轴进入磁场,经过磁场偏转后射出磁场而被收集(忽略粒子的重力和粒子之间的相互作用).
=4.0×106 C/kg,速度为v0=2.0×104 m/s带正电的粒子,粒子经过y轴进入磁场,经过磁场偏转后射出磁场而被收集(忽略粒子的重力和粒子之间的相互作用).
(1)当滑动头P在a端时,求粒子在磁场中做圆周运动的半径R0;
(2)当滑动头P在ab正中间时,求粒子射入磁场时速度的大小;
(3)滑动头P的位置不同则粒子在磁场中运动的时间也不同,求粒子在磁场中运动的最长时间.
如图8-3-24所示,在xOy平面内有足够大的匀强电场,电场方向竖直向上,电场强度E=40 N/C,在y轴左侧平面内有足够大的瞬时磁场,磁感应强度B1随时间t变化的规律如图乙所示,15π s后磁场消失,选定磁场垂直纸面向里为正方向.在y轴右侧平面内还有方向垂直纸面向外的恒定的匀强磁场,分布在一个半径为r=0.3 m的圆形区域(图中未画出),且圆的左侧与y轴相切,磁感应强度B2=0.8 T.t=0时刻,一质量m=8×10-4 kg\,电荷量q=2×10-4 C的微粒从x轴上xP=-0.8 m处的P点以速度v=0.12 m/s向x轴正方向入射.(g取10 m/s2,计算结果保留两位有效数字)


甲 乙
图8-3-24
(1)求微粒在第二象限运动过程中离y轴\,x轴的最大距离.
(2)若微粒穿过y轴右侧圆形磁场时,速度方向的偏转角度最大,求此圆形磁场的圆心坐标(x,y).
如图所示,磁感应强度为B=2.0×10-3 T的磁场分布在xOy平面上的MON三角形区域,其中M、N点距坐标原点O均为1.0 m,磁场方向垂直纸面向里.坐标原点O处有一个粒子源,不断地向xOy平面发射比荷为![]() =5×107 C/kg的带正电粒子,它们的速度大小都是v=5×104 m/s,与x轴正方向的夹角分布在0~90°范围内.
=5×107 C/kg的带正电粒子,它们的速度大小都是v=5×104 m/s,与x轴正方向的夹角分布在0~90°范围内.
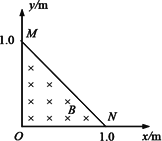
(1)求平行于x轴射入的粒子,出射点的位置及在磁场中运动时间;
(2)若从O点入射的与x轴正方向成![]() 角的粒子恰好不能从MN边射出,试画出此粒子运动的轨迹;
角的粒子恰好不能从MN边射出,试画出此粒子运动的轨迹;
(3)求能从直线MN射出的粒子,从粒子源O发射时的速度与x轴正向夹角范围.
(可供参考几个三角函数值sin41°=0.656,sin38°=0.616).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com