(12分)如图所示，物体A重100 N，物体B重20 N，A与水平桌面间的最大静摩擦力是30 N，整个系统处于静止状态，这时A受到的静摩擦力是多大？如果逐渐加大B的重力，而仍保持系统静止，则B物体重力的最大值是多少？

图2－17

【解析】：以结点O为研究对象，建立直角坐标系．

x轴上：

F_A＝Tcos45°①

y轴上：

F_B＝G_B＝Tsin45°②

①②联立，得

F_A＝G_Btan45°

代入其值得F_A＝20 N，以A为研究对象，受力分析，可得f_A＝F′_A＝F_A＝20 N，方向水平向右．当逐渐增大B的重力时，要使系统处于平衡状态，当A达到最大静摩擦力时，B物体的重力达到最大．由上述表达式可知：

G_Bm＝＝30 N

故A受到的静摩擦力为20 N，B物体的重力最大值为30 N.

(12分)如图所示，质量为5 kg的物块在水平拉力F＝15 N的作用下，从静止开始向右运动．物体与水平地面间的动摩擦因数μ＝0.2.求：

图3－17

(1)在力F的作用下，物体在前10 s内的位移；[来源:学+科+网]

(2)在t＝10 s末立即撤去力F，再经6 s物体还能运动多远？(g取10 m/s²)

【解析】：(1)物体在前10 s内受四个力：重力mg、支持力N、拉力F及滑动摩擦力f，如图所示．

根据牛顿第二定律有

N－mg＝0①

F－f＝ma₁②

又f＝μN③

联立解得

a₁＝＝ m/s²＝1 m/s²

由位移公式求出前10 s内的位移为

x₁＝a₁t²＝×1×10² m＝50 m.

(2)物体在10 s末的速度

v₁＝a₁t＝1×10 m/s＝10 m/s

10 s后物体做匀减速直线运动，其加速度大小为a₂＝＝μg＝0.2×10 m/s²＝2 m/s²

要考虑物体做匀减速运动最长能运动多长时间，设最长还能运动的时间为t′

t′＝＝ s＝5 s.

可见，物体经5 s就停下，故6 s内的位移[来源:Zxxk.Com]

x₂＝＝25 m.

(12分)一辆值勤的警车停在公路边，当警员发现从他旁边以v＝8 m/s的速度匀速行驶的货车有违章行为时，决定前去追赶，经2.5 s，警车发动起来，以加速度a＝2 m/s²做匀加速运动，试问：

(1)警车要经多长时间才能追上违章的货车？

(2)在警车追上货车之前，两车间的最大距离是多少？

【解析】：(1)设警车经过t时间追上货车，此时货车已行驶的位移x₁＝v(t＋2.5)①

警车的位移x₂＝at²②[来源:Z_xx_k.Com]

追上的条件是x₁＝x₂③

解①②③式得t＝10 s　t＝－2 s(舍去)．

(2)当两者速度相等时，两车距离最大

由v＝at′

得t′＝＝4 s

两车间最大距离为Δx＝v(t′＋2.5)－at′²＝36 m.

(12分)一重为G的小球，套于竖直放置的半径为R的光滑大圆环上，一劲度系数为k，自然长度L(L＜2R)的轻质弹簧，其上端固定在大圆环的最高点，下端与小球相连，如图4－19所示，不考虑一切摩擦．求小球静止时弹簧与竖直方向的夹角．(静止时弹簧不竖直)

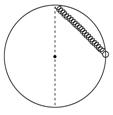
图4－19

【解析】：如图所示，连接BC，设弹簧与竖直方向夹角为θ，△ABC为直角三角形，AB＝2Rcosθ，弹簧弹力大小为F_弹＝k(2Rcosθ－L)．小球受力情况如图所示，球受三力作用：重力G、弹力F_弹、支持力N，球沿切线方向的合力为0，则

F_弹sinθ＝Gsin2θ

∴k(2Rcosθ－L)sinθ＝G·2sinθcosθ

整理可得：cosθ＝

所以θ＝arccos.

(12分)一重为G的小球，套于竖直放置的半径为R的光滑大圆环上，一劲度系数为k，自然长度L(L＜2R)的轻质弹簧，其上端固定在大圆环的最高点，下端与小球相连，如图4－19所示，不考虑一切摩擦．求小球静止时弹簧与竖直方向的夹角．(静止时弹簧不竖直)

图4－19

【解析】：如图所示，连接BC，设弹簧与竖直方向夹角为θ，△ABC为直角三角形，AB＝2Rcosθ，弹簧弹力大小为F_弹＝k(2Rcosθ－L)．小球受力情况如图所示，球受三力作用：重力G、弹力F_弹、支持力N，球沿切线方向的合力为0，则

F_弹sinθ＝Gsin2θ

∴k(2Rcosθ－L)sinθ＝G·2sinθcosθ

整理可得：cosθ＝

所以θ＝arccos.