
题目列表(包括答案和解析)
 分享到
分享到百度分享
一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,用下面的方法测量它匀速转动时的角速度。
实验器材:电磁打点计时器、米尺、纸带、复写纸片。
实验步骤:
(1)如图1所示,将电磁打点计时器固定在桌面上,将纸带的一端穿过打点计时器的限位孔后,固定在待测圆盘的侧面上,使得圆盘转动时,纸带可以卷在圆盘侧面上。
(2)启动控制装置使圆盘转动,同时接通电源,打点计时器开始打点。
(3)经过一段时间,停止转动和打点,取下纸带,进行测量。
① 由已知量和测得量表示的角速度的表达式为ω= 。式中各量的意义是:
.
② 某次实验测得圆盘半径r=5.50×10-2m,得到纸带的一段如图2所示,求得角速度为 。
(1) (2)6.8/s。 |
(10分)2008年9月25日至28日,我国在酒泉卫星发射中心成功发射了“神州七号”载人航天宇宙飞船,。承担此次飞行任务的航天员分别是翟志刚、刘伯明和景海鹏,
(1)如图所示,是A“神州七号”的火箭发射场,B为山区,C为城市,发射场正在进行发射,若长征二号F型火箭托着载人三名宇航员的“神舟七号”飞船向太空,已知火箭总长58.3m,发射塔的过程中,点火后,经7.0S火箭离开发射塔,设火箭的运动为匀加速运动,则在火箭离开发射塔的过程中(结果保留三位有效数字)火箭的加速度多大?
(2)质量为60kg的宇航员受到的飞船对他的作用力多大?(g=10m/s2)
(3)为了转播发射实况,我国科技工作者在发射场建立了发射台用于发射广播与电视信号。已知传输无线电广播所用的电磁波波长为550m,而传输电视信号所用的电磁波波长为0.556m,为了不让山区挡住信号的传播,使城市居民能听到和收看实况,必须通过在山顶的转发站来转发电视信号,这是因为什么呢?
(4)飞船在绕地球飞行的第五圈进行了变轨,由原来的椭圆轨道变为距地面高度为h的圆形轨道。则飞船在轨道上正常运行的速度是多大?飞船在轨道上运行周期是多少?质量为m0的宇航员,他在飞船中的重力将变为多大?(用已知量字母表示)
第Ⅰ卷(选择题 共31分)
一、单项选择题.本题共5小题,每小题3分,共计15分.每小题只有一个选项符合题意.
1. 关于科学家和他们的贡献,下列说法中正确的是[来源:Www..com]
A.安培首先发现了电流的磁效应
B.伽利略认为自由落体运动是速度随位移均匀变化的运动
C.牛顿发现了万有引力定律,并计算出太阳与地球间引力的大小
D.法拉第提出了电场的观点,说明处于电场中电荷所受到的力是电场给予的
2.如图为一种主动式光控报警器原理图,图中R1和R2为光敏电阻,R3和R4为定值电阻.当射向光敏电阻R1和R2的任何一束光线被遮挡时,都会引起警铃发声,则图中虚线框内的电路是
A.与门 B.或门 C.或非门 D.与非门
 | |||
 | |||
3.如图所示的交流电路中,理想变压器原线圈输入电压为U1,输入功率为P1,输出功率为P2,各交流电表均为理想电表.当滑动变阻器R的滑动头向下移动时
A.灯L变亮 B.各个电表读数均变大
C.因为U1不变,所以P1不变 D.P1变大,且始终有P1= P2
 4.竖直平面内光滑圆轨道外侧,一小球以某一水平速度v0从A点出发沿圆轨道运动,至B点时脱离轨道,最终落在水平面上的C点,不计空气阻力.下列说法中不正确的是
4.竖直平面内光滑圆轨道外侧,一小球以某一水平速度v0从A点出发沿圆轨道运动,至B点时脱离轨道,最终落在水平面上的C点,不计空气阻力.下列说法中不正确的是
A.在B点时,小球对圆轨道的压力为零
B.B到C过程,小球做匀变速运动
C.在A点时,小球对圆轨道压力大于其重力
D.A到B过程,小球水平方向的加速度先增加后减小
 5.如图所示,水平面上放置质量为M的三角形斜劈,斜劈顶端安装光滑的定滑轮,细绳跨过定滑轮分别连接质量为m1和m2的物块.m1在斜面上运动,三角形斜劈保持静止状态.下列说法中正确的是
5.如图所示,水平面上放置质量为M的三角形斜劈,斜劈顶端安装光滑的定滑轮,细绳跨过定滑轮分别连接质量为m1和m2的物块.m1在斜面上运动,三角形斜劈保持静止状态.下列说法中正确的是
A.若m2向下运动,则斜劈受到水平面向左摩擦力
B.若m1沿斜面向下加速运动,则斜劈受到水平面向右的摩擦力
C.若m1沿斜面向下运动,则斜劈受到水平面的支持力大于(m1+ m2+M)g
D.若m2向上运动,则轻绳的拉力一定大于m2g
二、多项选择题.本题共4小题,每小题4分,共计16分.每小题有多个选项符合题意.全部选对的得4分,选对但不全的得2分,错选或不答的得0分.
6.木星是太阳系中最大的行星,它有众多卫星.观察测出:木星绕太阳作圆周运动的半径为r1、 周期为T1;木星的某一卫星绕木星作圆周运动的半径为r2、 周期为T2.已知万有引力常量为G,则根据题中给定条件
A.能求出木星的质量
B.能求出木星与卫星间的万有引力
C.能求出太阳与木星间的万有引力
D.可以断定![]()
 7.如图所示,xOy坐标平面在竖直面内,x轴沿水平方向,y轴正方向竖直向上,在图示空间内有垂直于xOy平面的水平匀强磁场.一带电小球从O点由静止释放,运动轨迹如图中曲线.关于带电小球的运动,下列说法中正确的是
7.如图所示,xOy坐标平面在竖直面内,x轴沿水平方向,y轴正方向竖直向上,在图示空间内有垂直于xOy平面的水平匀强磁场.一带电小球从O点由静止释放,运动轨迹如图中曲线.关于带电小球的运动,下列说法中正确的是
A.OAB轨迹为半圆
B.小球运动至最低点A时速度最大,且沿水平方向
C.小球在整个运动过程中机械能守恒
D.小球在A点时受到的洛伦兹力与重力大小相等
 8.如图所示,质量为M、长为L的木板置于光滑的水平面上,一质量为m的滑块放置在木板左端,滑块与木板间滑动摩擦力大小为f,用水平的恒定拉力F作用于滑块.当滑块运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是
8.如图所示,质量为M、长为L的木板置于光滑的水平面上,一质量为m的滑块放置在木板左端,滑块与木板间滑动摩擦力大小为f,用水平的恒定拉力F作用于滑块.当滑块运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是
A.上述过程中,F做功大小为![]()
B.其他条件不变的情况下,F越大,滑块到达右端所用时间越长
C.其他条件不变的情况下,M越大,s越小
D.其他条件不变的情况下,f越大,滑块与木板间产生的热量越多
9.如图所示,两个固定的相同细环相距一定的距离,同轴放置,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量异种电荷.一带正电的粒子从很远处沿轴线飞来并穿过两环.则在带电粒子运动过程中
A.在O1点粒子加速度方向向左
B.从O1到O2过程粒子电势能一直增加
C.轴线上O1点右侧存在一点,粒子在该点动能最小
D.轴线上O1点右侧、O2点左侧都存在场强为零的点,它们关于O1、O2连线中点对称
 |
第Ⅱ卷(非选择题 共89分)
三、简答题:本题分必做题(第lO、11题)和选做题(第12题)两部分,共计42分.请将解答填写在答题卡相应的位置.
必做题
10.测定木块与长木板之间的动摩擦因数时,采用如图所示的装置,图中长木板水平固定.
 (1)实验过程中,电火花计时器应接在 ▲ (选填“直流”或“交流”)电源上.调整定滑轮高度,使 ▲ .
(1)实验过程中,电火花计时器应接在 ▲ (选填“直流”或“交流”)电源上.调整定滑轮高度,使 ▲ .
(2)已知重力加速度为g,测得木块的质量为M,砝码盘和砝码的总质量为m,木块的加速度为a,则木块与长木板间动摩擦因数μ= ▲ .
(3)如图为木块在水平木板上带动纸带运动打出的一条纸带的一部分,0、1、2、3、4、5、6为计数点,相邻两计数点间还有4个打点未画出.从纸带上测出x1=3.20cm,x2=4.52cm,x5=8.42cm,x6=9.70cm.则木块加速度大小a= ▲ m/s2(保留两位有效数字).
 |
11.为了测量某电池的电动势 E(约为3V)和内阻 r,可供选择的器材如下:
A.电流表G1(2mA 100Ω) B.电流表G2(1mA 内阻未知)
C.电阻箱R1(0~999.9Ω) D.电阻箱R2(0~9999Ω)
E.滑动变阻器R3(0~10Ω 1A) F.滑动变阻器R4(0~1000Ω 10mA)
G.定值电阻R0(800Ω 0.1A) H.待测电池
I.导线、电键若干
 (1)采用如图甲所示的电路,测定电流表G2的内阻,得到电流表G1的示数I1、电流表G2的示数I2如下表所示:
(1)采用如图甲所示的电路,测定电流表G2的内阻,得到电流表G1的示数I1、电流表G2的示数I2如下表所示:
| I1(mA) | 0.40 | 0.81 | 1.20 | 1.59 | 2.00 |
| I2(mA) | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 |
 |
根据测量数据,请在图乙坐标中描点作出I1—I2图线.由图得到电流表G2的内阻等于
▲ Ω.
(2)在现有器材的条件下,测量该电池电动势和内阻,采用如图丙所示的电路,图中滑动变阻器①应该选用给定的器材中 ▲ ,电阻箱②选 ▲ (均填写器材代号).
(3)根据图丙所示电路,请在丁图中用笔画线代替导线,完成实物电路的连接.
 | |||
 | |||
12.选做题(请从A、B和C三小题中选定两小题作答,并在答题卡上把所选题目对应字母后的方框涂满涂黑.如都作答,则按A、B两小题评分.)
A.(选修模块3-3)(12分)
(1)下列说法中正确的是 ▲
A.液体表面层分子间距离大于液体内部分子间距离,液体表面存在张力
B.扩散运动就是布朗运动
C.蔗糖受潮后会粘在一起,没有确定的几何形状,它是非晶体
D.对任何一类与热现象有关的宏观自然过程进行方向的说明,都可以作为热力学第二定律的表述
(2)将1ml的纯油酸加到500ml的酒精中,待均匀溶解后,用滴管取1ml油酸酒精溶液,让其自然滴出,共200滴.现在让其中一滴落到盛水的浅盘内,待油膜充分展开后,测得油膜的面积为200cm2,则估算油酸分子的大小是 ▲ m(保留一位有效数字).
 (3)如图所示,一直立的汽缸用一质量为m的活塞封闭一定量的理想气体,活塞横截面积为S,汽缸内壁光滑且缸壁是导热的,开始活塞被固定,打开固定螺栓K,活塞下落,经过足够长时间后,活塞停在B点,已知AB=h,大气压强为p0,重力加速度为g.
(3)如图所示,一直立的汽缸用一质量为m的活塞封闭一定量的理想气体,活塞横截面积为S,汽缸内壁光滑且缸壁是导热的,开始活塞被固定,打开固定螺栓K,活塞下落,经过足够长时间后,活塞停在B点,已知AB=h,大气压强为p0,重力加速度为g.
①求活塞停在B点时缸内封闭气体的压强;
②设周围环境温度保持不变,求整个过程中通过缸壁传递的热量Q(一定量理想气体的内能仅由温度决定).
B.(选修模块3-4)(12分)
(1)下列说法中正确的是 ▲
A.照相机、摄影机镜头表面涂有增透膜,利用了光的干涉原理
B.光照射遮挡物形成的影轮廓模糊,是光的衍射现象
 C.太阳光是偏振光
C.太阳光是偏振光
D.为了有效地发射电磁波,应该采用长波发射
(2)甲、乙两人站在地面上时身高都是L0, 甲、乙分别乘坐速度为0.6c和0.8c(c为光速)的飞船同向运动,如图所示.此时乙观察到甲的身高L ▲ L0;若甲向乙挥手,动作时间为t0,乙观察到甲动作时间为t1,则t1 ▲ t0(均选填“>”、“ =” 或“<”).
(3)x=0的质点在t=0时刻开始振动,产生的波沿x轴正方向传播,t1=0.14s时刻波的图象如图所示,质点A刚好开始振动.
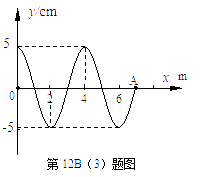 ①求波在介质中的传播速度;
①求波在介质中的传播速度;
②求x=4m的质点在0.14s内运动的路程.
C.(选修模块3-5)(12分)
(1)下列说法中正确的是 ▲
A.康普顿效应进一步证实了光的波动特性
B.为了解释黑体辐射规律,普朗克提出电磁辐射的能量是量子化的
C.经典物理学不能解释原子的稳定性和原子光谱的分立特征
D.天然放射性元素衰变的快慢与化学、物理状态有关
(2)![]() 是不稳定的,能自发的发生衰变.
是不稳定的,能自发的发生衰变.
①完成![]() 衰变反应方程
衰变反应方程 ![]() ▲ .
▲ .
②![]() 衰变为
衰变为![]() ,经过 ▲ 次α衰变, ▲ 次β衰变.
,经过 ▲ 次α衰变, ▲ 次β衰变.
(3)1919年,卢瑟福用α粒子轰击氮核发现质子.科学研究表明其核反应过程是:α粒子轰击静止的氮核后形成了不稳定的复核,复核发生衰变放出质子,变成氧核.设α粒子质量为m1,初速度为v0,氮核质量为m2,质子质量为m0, 氧核的质量为m3,不考虑相对论效应.
①α粒子轰击氮核形成不稳定复核的瞬间,复核的速度为多大?
②求此过程中释放的核能.
四、计算题:本题共3小题,共计47分.解答时请写出必要的文字说明、方程式和重要的演算步骤,只写出最后答案的不能得分,有数值计算的题,答案中必须明确写出数值和单位.
13.如图所示,一质量为m的氢气球用细绳拴在地面上,地面上空风速水平且恒为v0,球静止时绳与水平方向夹角为α.某时刻绳突然断裂,氢气球飞走.已知氢气球在空气中运动时所受到的阻力f正比于其相对空气的速度v,可以表示为f=kv(k为已知的常数).则
(1)氢气球受到的浮力为多大?
(2)绳断裂瞬间,氢气球加速度为多大?
(3)一段时间后氢气球在空中做匀速直线运动,其水平方向上的速度与风速v0相等,求此时气球速度大小(设空气密度不发生变化,重力加速度为g).
 |
14.如图所示,光滑绝缘水平面上放置一均匀导体制成的正方形线框abcd,线框质量为m,电阻为R,边长为L.有一方向竖直向下的有界磁场,磁场的磁感应强度为B,磁场区宽度大于L,左边界与ab边平行.线框在水平向右的拉力作用下垂直于边界线穿过磁场区.
(1)若线框以速度v匀速穿过磁场区,求线框在离开磁场时ab两点间的电势差;
(2)若线框从静止开始以恒定的加速度a运动,经过t1时间ab边开始进入磁场,求cd边将要进入磁场时刻回路的电功率;
(3)若线框以初速度v0进入磁场,且拉力的功率恒为P0.经过时间T,cd边进入磁场,此过程中回路产生的电热为Q.后来ab边刚穿出磁场时,线框速度也为v0,求线框穿过磁场所用的时间t.

15.如图所示,有界匀强磁场的磁感应强度为B,方向垂直纸面向里,MN为其左边界,磁场中放置一半径为R的圆柱形金属圆筒,圆心O到MN的距离OO1=2R,圆筒轴线与磁场平行.圆筒用导线通过一个电阻r0接地,最初金属圆筒不带电.现有范围足够大的平行电子束以速度v0从很远处沿垂直于左边界MN向右射入磁场区,已知电子质量为m,电量为e.
(1)若电子初速度满足![]() ,则在最初圆筒上没有带电时,能够打到圆筒上的电子对应MN边界上O1两侧的范围是多大?
,则在最初圆筒上没有带电时,能够打到圆筒上的电子对应MN边界上O1两侧的范围是多大?
(2)当圆筒上电量达到相对稳定时,测量得到通过电阻r0的电流恒为I,忽略运动电子间的相互作用,求此时金属圆筒的电势φ和电子到达圆筒时速度v(取无穷远处或大地电势为零).
(3)在(2)的情况下,求金属圆筒的发热功率.
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com