进行“验证机械能守恒定律”的实验:

(1)现有以下器材:带铁夹的铁架台,打点计时器以及复写纸、纸带,导线,还需要的器材是
刻度尺
刻度尺
、
带铁夹的重物
带铁夹的重物
、
低压交流电源
低压交流电源
;
(2)下列选项中,属于系统误差的是
AE
AE
;属于偶然误差的是
B
B
;
A.打点计时器对纸带的阻力
B.测量纸带上的点距时存在的误差
C.测量点距时,将6个点误计为7个点
D.用秒表测量下落时间,由公式h=
gt2算出重物下落的高度
E.重物和纸带下落过程中受到空气阻力
(3)选出一条纸带如图1所示,其中O点为打点计时器打下的第一个点,A、B、C为三个计数点,打点计时器通以50Hz的交流电.用刻度尺测得OA=12.41cm,OB=19.10cm,OC=27.29cm,在计数点A和B、B和C之间还各有一个点,重物的质量为1.00kg,取g=9.80m/s
2.甲同学根据以上数据算出:当打点计时器打到B点时重物的重力势能比开始下落时减少了
1.87
1.87
J;此时重物的动能比开始下落时增加了
1.73
1.73
J.(结果均保留三位有效数字). 实验结论是
在误差允许范围内,重物的机械能守恒
在误差允许范围内,重物的机械能守恒
.
(4)乙同学利用他自己实验时打出的纸带,测量出了各计数点到打点计时器打下的第一个点的距离h,算出了各计数点对应的速度v,以h为横轴,以
v2为纵轴画出了如图2的图线.图线的斜率数值上近似等于(填代号)
B
B
A.3.60 B.9.80 C.4.90
图线未过原点O的原因是
操作中先释放重物,再接通(打点计时器)电源
操作中先释放重物,再接通(打点计时器)电源
.



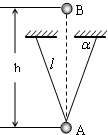
 如图所示为一双线摆,它是由两根等长细绳悬挂一小球而构成的,绳的质量可以忽略.已知两绳长均为l,绳与水平方向夹角为α,当摆球A垂直于纸面做简谐运动经过平衡位置时,另一个小球B从A球的正上方开始做自由落体运动,且正好打在A球上,则小球B距平衡位置高度h可能为多少?
如图所示为一双线摆,它是由两根等长细绳悬挂一小球而构成的,绳的质量可以忽略.已知两绳长均为l,绳与水平方向夹角为α,当摆球A垂直于纸面做简谐运动经过平衡位置时,另一个小球B从A球的正上方开始做自由落体运动,且正好打在A球上,则小球B距平衡位置高度h可能为多少?
 ,A球从平衡位置经过
,A球从平衡位置经过 再次回到平衡位置时与B球相碰则tA=
再次回到平衡位置时与B球相碰则tA= =π
=π (1)
(1) gtB2 (2);
gtB2 (2); 