
题目列表(包括答案和解析)
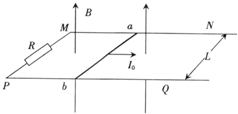 如图所示,足够长的金属导轨MN和PQ与R相连,平行地放在水平桌面上,质量为m的金属杆可以无摩擦地沿导轨运动.导轨与ab杆的电阻不计,导轨宽度为L,磁感应强度为B的匀强磁场垂直穿过整个导轨平面.现给金属杆ab一个初速度V0,使ab杆向右滑行.
如图所示,足够长的金属导轨MN和PQ与R相连,平行地放在水平桌面上,质量为m的金属杆可以无摩擦地沿导轨运动.导轨与ab杆的电阻不计,导轨宽度为L,磁感应强度为B的匀强磁场垂直穿过整个导轨平面.现给金属杆ab一个初速度V0,使ab杆向右滑行.如图所示,足够长的金属导轨MN和PQ与R相连,平行地放在水平桌面上,质量为m的金属杆可以无摩擦地沿导轨运动.导轨与ab杆的电阻不计,导轨宽度为L,磁感应强度为B的匀强磁场垂直穿过整个导轨平面.现给金属杆ab一个瞬时冲量I0,使ab杆向右滑行.
(1)求回路的最大电流.
(2)当滑行过程中电阻上产生的热量为Q时,杆ab的加速度多大?
(3)杆ab从开始运动到停下共滑行了多少距离?
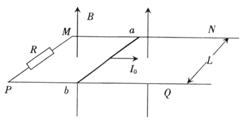
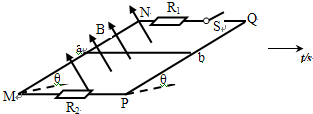 如图所示,足够长的金属导轨MN、PQ平行放置,间距为L,与水平面成θ角,导轨与定值电阻R1和R2相连,且R1=R2=R,R1支路串联开关S,原来S闭合.匀强磁场垂直导轨平面向上,有一质量为m、有效电阻也为R的导体棒ab与导轨垂直放置,它与导轨的接触粗糙且始终接触良好,现让导体棒ab从静止开始释放,沿导轨下滑,当导体棒运动达到稳定状态时速率为V,此时整个电路消耗的电功率为重力功率的
如图所示,足够长的金属导轨MN、PQ平行放置,间距为L,与水平面成θ角,导轨与定值电阻R1和R2相连,且R1=R2=R,R1支路串联开关S,原来S闭合.匀强磁场垂直导轨平面向上,有一质量为m、有效电阻也为R的导体棒ab与导轨垂直放置,它与导轨的接触粗糙且始终接触良好,现让导体棒ab从静止开始释放,沿导轨下滑,当导体棒运动达到稳定状态时速率为V,此时整个电路消耗的电功率为重力功率的| 3 | 4 |
 .已知重力加速度为g,导轨电阻不计,求:
.已知重力加速度为g,导轨电阻不计,求: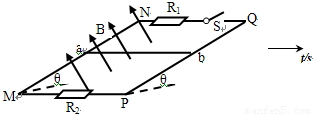
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com