
题目列表(包括答案和解析)
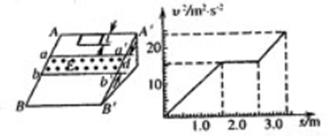
如图所示,一个质量m=0.1 kg、阻值R=0.5Ω的正方形金属框,放在表面绝缘且光滑的斜面顶端(框上边与从AA‘重合),自静止开始沿斜面下滑,下滑过程中穿过一段边界与斜面底边BB‘平行、宽度为d的匀强磁场后滑至斜面底端(框下边与BB‘重合)。设金属在下滑过程中的速度为v时所对应的位移为s,那么v2—s图象如图所示,已知匀强磁场方向垂直斜面向上。试问:
(1)根据v2—s图象所提供的信息,计算出斜面倾角![]() 和匀强磁场的宽度d。
和匀强磁场的宽度d。
(2)匀强磁场的磁感应强度为多大?金属框从斜面顶端滑至底端所需的时间为多少?
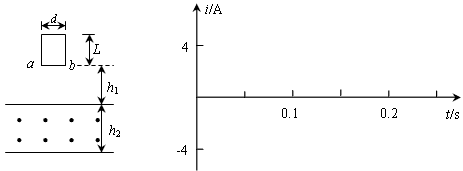
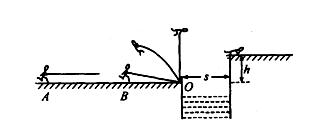
如图所示,一位质量m=60 kg,参加“挑战极限运动”的业余选手,要越过一宽为s = 2.5 m的水沟后跃上高为h=2.0 m的平台。他采用的方法是:手握一根长L=3.25 m的轻质弹性杆一端,从A点由静止开始加速助跑,至B点时杆另一端抵在O点的阻挡物上,接着杆发生形变,同时人蹬地后被弹起,到达最高点时杆处于竖直状态,人的重心在杆的顶端,此刻人放开杆水平飞出并趴落到平台上,运动过程中空气阻力可忽略不计。(g取10m/s2)求:
(1)人要最终到达平台,在最高点飞出时刻的速度![]() 应至少多大?
应至少多大?
(2) 设人到达B点时速度![]() =8 m/s ,人受的阻力为体重的0.1倍,助跑距离
=8 m/s ,人受的阻力为体重的0.1倍,助跑距离![]() =16 m ,则人在该过程中做的功为多少?
=16 m ,则人在该过程中做的功为多少?
(3)设人跑动过程中重心离地高度H=0. 8 m,在(1)、(2)两问的条件下,人要越过一宽为s = 2.5 m的水沟后跃上高为h=2.0 m的平台,在整个过程中人应至少要做多少功?
如图所示,一位质量m=60 kg,参加“挑战极限运动”的业余选手,要越过一宽为s = 2.5 m的水沟后跃上高为h=2.0 m的平台。他采用的方法是:手握一根长L=3.25 m的轻质弹性杆一端,从A点由静止开始加速助跑,至B点时杆另一端抵在O点的阻挡物上,接着杆发生形变,同时人蹬地后被弹起,到达最高点时杆处于竖直状态,人的重心在杆的顶端,此刻人放开杆水平飞出并趴落到平台上,运动过程中空气阻力可忽略不计。(g取10m/s2)求:
(1)人要最终到达平台,在最高点飞出时刻的速度![]() 应至少多大?
应至少多大?
(2) 设人到达B点时速度![]() =8 m/s ,人受的阻力为体重的0.1倍,助跑距离
=8 m/s ,人受的阻力为体重的0.1倍,助跑距离![]() =16 m ,则人在该过程中做的功为多少?
=16 m ,则人在该过程中做的功为多少?
(3)设人跑动过程中重心离地高度H=0. 8 m,在(1)、(2)两问的条件下,人要越过一宽为s= 2.5 m的水沟后跃上高为h=2.0 m的平台,在整个过程中人应至少要做多少功?
如图所示,一位质量m="60" kg,参加“挑战极限运动”的业余选手,要越过一宽为s =" 2.5" m的水沟后跃上高为h="2.0" m的平台。他采用的方法是:手握一根长L="3.25" m的轻 质弹性杆一端,从A点由静止开始加速助跑,至B点时杆另一端抵在O点的阻挡物上,接着杆发生形变,同时人蹬地后被弹起,到达最高点时杆处于竖直状态,人的重心在杆的
质弹性杆一端,从A点由静止开始加速助跑,至B点时杆另一端抵在O点的阻挡物上,接着杆发生形变,同时人蹬地后被弹起,到达最高点时杆处于竖直状态,人的重心在杆的 顶端,此刻人放开杆水平飞出并趴落到平台上,运动过程中空气阻力可忽略不计。(g取10m/s2)求:
顶端,此刻人放开杆水平飞出并趴落到平台上,运动过程中空气阻力可忽略不计。(g取10m/s2)求:
(1)人要最终到达平台,在最高点飞出时刻的速度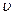 应至少
应至少 多大?
多大?
(2) 设人到达B点时速度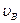 ="8" m/s ,人受的阻力为体重的0.1倍,助跑距离
="8" m/s ,人受的阻力为体重的0.1倍,助跑距离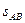 ="16" m ,则人在该过程中做的功为多少?
="16" m ,则人在该过程中做的功为多少?
(3)设人跑动过程中重心离地高度H="0." 8 m,在(1)、(2)两问的条件下,人要越过一宽为s =" 2.5" m的水沟后跃上高为h="2.0" m的平台,在整个过程中人应至少要做多少功?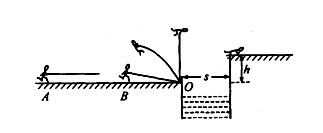
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com