
题目列表(包括答案和解析)
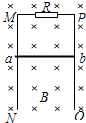 如图所示,足够长的光滑平行金属导轨MN、PQ竖直放置,一匀强磁场垂直穿过导轨平面,导轨的上端M与P间连接阻值为R=0.40Ω的电阻,质量为m=0.01kg、电阻为r=0.30Ω的金属棒ab紧贴在导轨上.现使金属棒ab由静止开始下滑,其下滑距离与时间的关系如下表所示,导轨电阻不计,试求:
如图所示,足够长的光滑平行金属导轨MN、PQ竖直放置,一匀强磁场垂直穿过导轨平面,导轨的上端M与P间连接阻值为R=0.40Ω的电阻,质量为m=0.01kg、电阻为r=0.30Ω的金属棒ab紧贴在导轨上.现使金属棒ab由静止开始下滑,其下滑距离与时间的关系如下表所示,导轨电阻不计,试求:| 时 间t(s) | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 |
| 下滑距离s(m) | 0 | 0.1 | 0.3 | 0.7 | 1.4 | 2.1 | 2.8 | 3.5 |
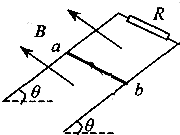 如图所示,足够长的光滑平行金属导轨,相距上,导轨平面与水平面夹角为θ,匀强磁场垂直于导轨平面,已知磁感应强度为B,平行导轨的上端连接一个阻值为R的电阻.一根质量为m,电阻为
如图所示,足够长的光滑平行金属导轨,相距上,导轨平面与水平面夹角为θ,匀强磁场垂直于导轨平面,已知磁感应强度为B,平行导轨的上端连接一个阻值为R的电阻.一根质量为m,电阻为| 1 | 2 |
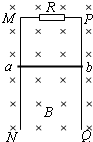 如图所示,足够长的光滑平行金属导轨MN、PQ竖直放置,磁感应强度B=0.50T的匀强磁场垂直穿过导轨平面,导轨的上端M与P间连接阻值为R=0.50Ω的电阻,导轨宽度L=0.40m.金属棒ab紧贴在导轨上,现使金属棒ab由静止开始下滑,通过传感器记录金属棒ab下滑的距离h与时间t的关系如下表所示.(金属棒ab和导轨电阻不计,g=10m/s2)
如图所示,足够长的光滑平行金属导轨MN、PQ竖直放置,磁感应强度B=0.50T的匀强磁场垂直穿过导轨平面,导轨的上端M与P间连接阻值为R=0.50Ω的电阻,导轨宽度L=0.40m.金属棒ab紧贴在导轨上,现使金属棒ab由静止开始下滑,通过传感器记录金属棒ab下滑的距离h与时间t的关系如下表所示.(金属棒ab和导轨电阻不计,g=10m/s2)| 时 间t/s | 0 | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 | 1.20 | 1.40 | 1.60 | 1.80 |
| 下滑距离h/m | 0 | 0.18 | 0.60 | 1.20 | 1.95 | 2.80 | 3.80 | 4.80 | 5.80 | 6.80 |
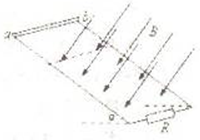 如图所示,足够长的光滑平行金属导轨,间距为L=2.0m,导轨平面与水平方向成α=30°角.导轨下部接有一只阻值为R=5.0Ω的电阻.现将一个长也是L=2.0m,质量为m=0.20kg的金属棒自导轨顶部从静止开始沿导轨自由下滑.下滑一段距离后进入一个垂直于导轨平面向下的匀强磁场中,磁感应强度B=0.50T,该磁场下部无边界.金属棒进入磁场后又下滑了s=30m后开始做匀速运动.在做匀速运动之前,电阻R上产生的电热是60J.金属导轨和金属棒的电阻不计.
如图所示,足够长的光滑平行金属导轨,间距为L=2.0m,导轨平面与水平方向成α=30°角.导轨下部接有一只阻值为R=5.0Ω的电阻.现将一个长也是L=2.0m,质量为m=0.20kg的金属棒自导轨顶部从静止开始沿导轨自由下滑.下滑一段距离后进入一个垂直于导轨平面向下的匀强磁场中,磁感应强度B=0.50T,该磁场下部无边界.金属棒进入磁场后又下滑了s=30m后开始做匀速运动.在做匀速运动之前,电阻R上产生的电热是60J.金属导轨和金属棒的电阻不计. 如图所示,足够长的光滑平行金属导轨MN、PQ竖直放置,导轨间距0.40m.一个磁感应强度B=0.50T的匀强磁场垂直穿过导轨平面,导轨的上端M与P间连接阻值为R=0.30Ω的电阻;长L=0.40m、电阻r=0.20Ω的金属棒ab紧贴在导轨上.现使金属棒ab由静止开始下滑,通过传感器记录金属棒ab相对于出发点下滑的距离s,s与下滑时间,的关系如下表所示,导轨电阻不计,g=l0m/s2.求:
如图所示,足够长的光滑平行金属导轨MN、PQ竖直放置,导轨间距0.40m.一个磁感应强度B=0.50T的匀强磁场垂直穿过导轨平面,导轨的上端M与P间连接阻值为R=0.30Ω的电阻;长L=0.40m、电阻r=0.20Ω的金属棒ab紧贴在导轨上.现使金属棒ab由静止开始下滑,通过传感器记录金属棒ab相对于出发点下滑的距离s,s与下滑时间,的关系如下表所示,导轨电阻不计,g=l0m/s2.求:| 时间t(s) | 0 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 |
| 下滑距离s (m) | 0 | 0.04 | 0.14 | 0.35 | 0.60 | 0.85 | 1.10 | 1.35 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com