
题目列表(包括答案和解析)
如图6-1-2所示,厚度为h、宽度为d的导体板放在垂直于它的磁感应强度为B的均匀磁场中,当电流通过导体板时,在导体板的上侧面A和下侧面![]() 之间会产生电势差,这种现象称为霍尔效应.实验表明,当磁场不太强时,电势差U、电流I和B的关系为U=k
之间会产生电势差,这种现象称为霍尔效应.实验表明,当磁场不太强时,电势差U、电流I和B的关系为U=k![]() 式中的比例系数k称为霍尔系数.
式中的比例系数k称为霍尔系数.
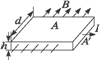
霍尔效应可解释如下:外部磁场的洛伦兹力使运动的电子聚集在导体板的一侧,在导体板的另一侧会出现多余的正电荷,从而形成横向电场.横向电场对电子施加与洛伦兹力方向相反的静电力.当静电力与洛伦兹力达到平衡时,导体板上下两侧之间就会形成稳定的电势差.
设电流I是由电子的定向流动形成的,电子的平均定向速度为v,电荷量为e,回答下列问题:
(1)达到稳定状态时,导体板上侧面A的电势_________(填“高于”“低于”或“等于”)下侧面![]() 的电势.
的电势.
(2)电子所受的洛伦兹力的大小为_________.
(3)当导体板上下两侧面之间的电势差为U时,电子所受静电力的大小为_________.
(4)由静电力和洛伦兹力平衡的条件,证明霍尔系数k=![]() ,其中n代表导体板单位体积中电子的个数.
,其中n代表导体板单位体积中电子的个数.
t1时刻通过线圈的磁通量为零
t2时刻通过线圈的磁通量的绝对值最大
t3时刻通过线圈的磁通量变化率的绝对值最大
每当e变换方向时,通过线圈的磁通量绝对值都为最大
如图9-2-20甲所示线圈的匝数n=100匝,横截面积S=50 cm2,线圈总电阻r=10 Ω,沿轴向有匀强磁场,设图示磁场方向为正,磁场的磁感应强度随时间作如图乙所示变化,则在开始的0.1 s内 ( ).

图9-2-20
A.磁通量的变化量为0.25 Wb
B.磁通量的变化率为2.5×10-2 Wb/s
C.a、b间电压为0
D.在a、b间接一个理想电流表时,电流表的示数为0.25 A
如图9-2-26甲所示,空间存在一宽度为2L的有界匀强磁场,磁场方向垂直纸面向里.在光滑绝缘水平面内有一边长为L的正方形金属线框,其质量m=1 kg、电阻R=4 Ω,在水平向左的外力F作用下,以初速度v0=4 m/s匀减速进入磁场,线框平面与磁场垂直,外力F大小随时间t变化的图线如图乙所示.以线框右边刚进入磁场时开始计时.
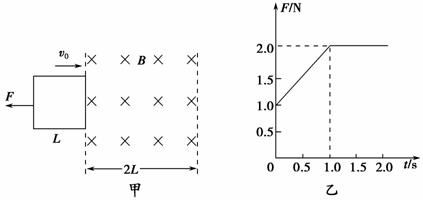
图9-2-26
(1)求匀强磁场的磁感应强度B;
(2)求线框进入磁场的过程中,通过线框的电荷量q;
(3)判断线框能否从右侧离开磁场?说明理由.
电子感应加速器是利用变化磁场产生的电场来加速电子的.如图K51-6所示,在圆形磁铁的两极之间有一环形真空室,用交变电流励磁的电磁铁在两极间产生交变磁场,从而在环形室内产生很强的电场,使电子加速.被加速的电子同时在洛伦兹力的作用下沿圆形轨道运动.设法把高能电子引入靶室,就能进一步进行实验工作.已知在一个轨道半径为r=0.84 m的电子感应加速器中,电子在被加速的4.2 ms内获得的能量为120 MeV.设在这期间电子轨道内的高频交变磁场是线性变化的,磁通量的最小值为零,最大值为1.8 Wb,试求电子在加速器中共绕行了多少周?

可控热核聚变反应堆产生能量的方式和太阳类似,因此,它被俗称为“人造太阳”.热核反应的发生需要几百万度以上的高温,因而反应中的大量![]() 带电粒子没有通常意义上的容器可装.人类正在积极探索各种约束装置,磁约束托卡马克装置就是其中一种.如图K38-12所示为该装置的简化模型.有一个圆环形区域,区域内有垂直纸面向里的匀强磁场,已知其截面
带电粒子没有通常意义上的容器可装.人类正在积极探索各种约束装置,磁约束托卡马克装置就是其中一种.如图K38-12所示为该装置的简化模型.有一个圆环形区域,区域内有垂直纸面向里的匀强磁场,已知其截面![]() 内半径为R1=1.0 m,磁感应强度为B=1.0 T,被约束粒子的比荷为
内半径为R1=1.0 m,磁感应强度为B=1.0 T,被约束粒子的比荷为![]() =4.0×107 C/kg,该带电粒子从中空区域与磁场交界面上的P点以速度v0=4.0×107 m/s沿环的半径方向射入磁场(不计带电粒子在运动过程中的相互作用,不计带电粒子的重力).
=4.0×107 C/kg,该带电粒子从中空区域与磁场交界面上的P点以速度v0=4.0×107 m/s沿环的半径方向射入磁场(不计带电粒子在运动过程中的相互作用,不计带电粒子的重力).
(1)为约束粒子不穿越磁场外边界,求磁场区域的最小外半径R2.
(2)若改变该粒子的入射速率v,使v=![]() v0,求该粒子从P点进入磁场开始到第一次回到P点所需要的时间t.
v0,求该粒子从P点进入磁场开始到第一次回到P点所需要的时间t.
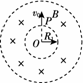
图K38-12
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com