
题目列表(包括答案和解析)
 倾角为θ的固定斜面顶端有一滑轮,细线跨过滑轮连接A、B两个质量均为m的物块.让A物块静止在斜面底端,拉A的细线与斜面平行,B物块悬挂在离地面h高处,如图所示.斜面足够长,物块与斜面间的动摩擦因数为μ,不计其它阻力.释放后B物块下落A物块沿斜面上滑.
倾角为θ的固定斜面顶端有一滑轮,细线跨过滑轮连接A、B两个质量均为m的物块.让A物块静止在斜面底端,拉A的细线与斜面平行,B物块悬挂在离地面h高处,如图所示.斜面足够长,物块与斜面间的动摩擦因数为μ,不计其它阻力.释放后B物块下落A物块沿斜面上滑.| mv2 |
| 2 |
| v |
| a |
| mv2 |
| 2 |
| v |
| a |
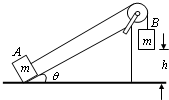
 倾角为θ的固定斜面顶端有一滑轮,细线跨过滑轮连接A、B两个质量均为m的物块.让A物块静止在斜面底端,拉A的细线与斜面平行,B物块悬挂在离地面h高处,如图所示.斜面足够长,物块与斜面间的动摩擦因数为μ,不计其它阻力.释放后B物块下落A物块沿斜面上滑.
倾角为θ的固定斜面顶端有一滑轮,细线跨过滑轮连接A、B两个质量均为m的物块.让A物块静止在斜面底端,拉A的细线与斜面平行,B物块悬挂在离地面h高处,如图所示.斜面足够长,物块与斜面间的动摩擦因数为μ,不计其它阻力.释放后B物块下落A物块沿斜面上滑. ,从中解出v;
,从中解出v; ,代入数值可求得t.
,代入数值可求得t.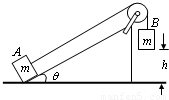 倾角为θ的固定斜面顶端有一滑轮,细线跨过滑轮连接A、B两个质量均为m的物块.让A物块静止在斜面底端,拉A的细线与斜面平行,B物块悬挂在离地面h高处,如图所示.斜面足够长,物块与斜面间的动摩擦因数为μ,不计其它阻力.释放后B物块下落A物块沿斜面上滑.
倾角为θ的固定斜面顶端有一滑轮,细线跨过滑轮连接A、B两个质量均为m的物块.让A物块静止在斜面底端,拉A的细线与斜面平行,B物块悬挂在离地面h高处,如图所示.斜面足够长,物块与斜面间的动摩擦因数为μ,不计其它阻力.释放后B物块下落A物块沿斜面上滑.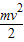 ,从中解出v;
,从中解出v;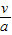 ,代入数值可求得t.
,代入数值可求得t.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com