练习册

  • 练习册
  • 试题
    2．子弹打木块类问题 子弹打木块实际上是一种完全非弹性碰撞.作为一个典型.它的特点是:子弹以水平速度射向原来静止的木块.并留在木块中跟木块共同运动.下面从动量.能量和牛顿运动定律等多个角度来分析这一过程. [例3] 设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块.并留在木块中不再射出.子弹钻入木块深度为d.求木块对子弹的平均阻力的大小和该过程中木块前进的距离. 解析:子弹和木块最后共同运动.相当于完全非弹性碰撞. 从动量的角度看.子弹射入木块过程中系统动量守恒: 从能量的角度看.该过程系统损失的动能全部转化为系统的内能.设平均阻力大小为f.设子弹.木块的位移大小分别为s1.s2.如图所示.显然有s1-s2=d 对子弹用动能定理: --① 对木块用动能定理: --② ①.②相减得: --③ 点评:这个式子的物理意义是:fžd恰好等于系统动能的损失,根据能量守恒定律.系统动能的损失应该等于系统内能的增加,可见.即两物体由于相对运动而摩擦产生的热.等于摩擦力大小与两物体相对滑动的路程的乘积(由于摩擦力是耗散力.摩擦生热跟路径有关.所以这里应该用路程.而不是用位移). 由上式不难求得平均阻力的大小: 至于木块前进的距离s2.可以由以上②.③相比得出: 从牛顿运动定律和运动学公式出发.也可以得出同样的结论.由于子弹和木块都在恒力作用下做匀变速运动.位移与平均速度成正比: 一般情况下.所以s2<<d.这说明.在子弹射入木块过程中.木块的位移很小.可以忽略不计.这就为分阶段处理问题提供了依据.象这种运动物体与静止物体相互作用.动量守恒.最后共同运动的类型.全过程动能的损失量可用公式:-④ 当子弹速度很大时.可能射穿木块.这时末状态子弹和木块的速度大小不再相等.但穿透过程中系统动量仍然守恒.系统动能损失仍然是ΔEK= f žd(这里的d为木块的厚度).但由于末状态子弹和木块速度不相等.所以不能再用④式计算ΔEK的大小. 【查看更多】

     

    题目列表(包括答案和解析)

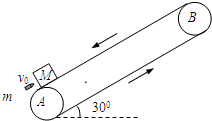    （2009?孝感模拟）某兴趣小组设计了一种测量子弹射出枪口时速度大小的方法．在离地面高度为h的光滑水平桌面上放置一木块，将枪口靠近木块水平射击，子弹嵌入木块后与木块一起水平飞出，落地点与桌边缘的水平距离是s1；然后将木块重新放回原位置，再打一枪，子弹与木块的落地点与桌边的水平距离是s2，求子弹射出枪口时速度的大小．

    查看答案和解析>>

    （2011?攀枝花三模）如图所示，传送带AB长L=5m，与水平方向的夹角为30°．质量为M=1kg的小木块随传送带一起以v1=4m/s的速度向下匀速运动（传送带的传送速度恒定），小木块与传送带间刚好不打滑．当小木块运动至最下端A点时，一颗质量为m=0.02kg的子弹，沿平行于传送带方向，以v0=600m/s的速度正对小木块射入并穿出，穿出速度u=100m/s，以后每隔1s就有一颗子弹射向小木块．设子弹射穿小木块的时间极短，且每次穿过小木块时所受阻力相同（g取10m/s2），小木块与传送带间滑动摩擦力等于最大静摩擦力．求：
    （1）在第一颗子弹穿出小木块时，小木块的速度是多大？
    （2）小木块被多少颗子弹打穿后能够从传送带B端飞出？飞出速度为多大？
    （3）小木块从A点运动到B点过程中，小木块与传送带间的摩擦力做功产生的热量为多少？

    查看答案和解析>>

    将质量为M的木块固定在光滑水平面上，一颗质量为m的子弹以速度υ0沿水平方向射入木块，子弹射穿木块时的速度为
    v0
    3
    ，现将同样的木块放在光滑的水平桌面上，相同的子弹仍以速度υ0沿水平方向射入木块，则以下说法正确的是（　　）

    查看答案和解析>>

    质量为10 g的子弹，以300 m/s的水平初速度射入一块竖直固定的木板，把木板打穿，子弹射出的速度为200 m/s.若板的厚度为10 cm，试求子弹对木块的平均作用力.

    查看答案和解析>>

    某学生实验小组为了搞清楚功、能、动量之间的关系，设计了如下实验：

    ㈠主要实验器材：一块正方形的软木块，其边长D=16cm，质量M=40g；一支出射速度能够连续可调的气枪，其子弹的质量m=10g；……

    ㈡主要实验过程：首先，他们把正方形的软木块固定在桌面上，当子弹以20m/s的水平速度从正面射入该木块后，实验小组测得了子弹能够进入木块中5cm的深度。然后，他们把该木块放在光滑的水平面上（例如气垫导轨上），子弹再次从正面射入该木块，……。在后者情况下，请你利用力学知识，帮助他们分析和预测以下几个问题：⑴若子弹仍以20m/s的水平速度射入木块，子弹最多能进入木块中的深度有多大？⑵若子弹仍以20m/s的水平速度射入木块，在子弹射入木块的过程中，系统损失的机械能和产生的热量各是多少？⑶为了使子弹能够穿透该木块，那么子弹的入射速度大小不能低于多少？

    查看答案和解析>>


    同步练习册答案