
题目列表(包括答案和解析)
如图所示,质量分别为2 m和3m的两个小球固定在一根直角尺的两端A、B,直角尺的顶点O处有光滑的固定转动轴。AO、BO的长分别为2L和L。开始时直角尺的AO部分处于水平位置而B在O的正下方。让该系统由静止开始自由转动,求:⑴当A到达最低点时,A小球的速度大小v;⑵ B球能上升的最大高度h;⑶开始转动后B球可能达到的最大速度vm。
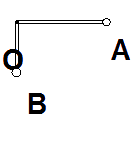
如图所示,质量为3m的足够长木板 C 静止在光滑水平面上,质量均为 m 的两个物体 A、B 放在 C 的左端,A、B 间相距 s0,现同时对A、B施加水平向右的瞬间冲量而使之分别获得初速度v0和2v0,若A、B与C之间的动摩擦因数分别为 μ 和 2 μ ,则:
(1)最终A、B、C的共同速度为多大
(2)求A达到最小速度时,系统产生的热量Q。

如图所示,质量为3m的足够长木板 C 静止在光滑水平面上,质量均为 m 的两个物体 A、B 放在 C 的左端,A、B 间相距 s0,现同时对A、B施加水平向右的瞬间冲量而使之分别获得初速度v0和2v0,若A、B与C之间的动摩擦因数分别为 μ 和 2 μ ,则:
(1)最终A、B、C的共同速度为多大
(2)求A达到最小速度时,系统产生的热量Q。

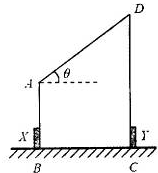
(18分)如图所示,质量足够大、截面是直角梯形的物块静置在光滑水平地面上,其两个侧面恰好与两个固定在地面上的压力传感器X、Y相接触。图中AB高H=0.3m,AD长L=0.5m。斜面倾角 。可视为质点的小物块P(图中未画出)质量m=1kg,它与斜面的动摩擦因数
。可视为质点的小物块P(图中未画出)质量m=1kg,它与斜面的动摩擦因数 可以通过更换斜面表面的材料进行调节,调节范围是
可以通过更换斜面表面的材料进行调节,调节范围是 。
。


(1)令 ,将P由D点静止释放,求P在斜面上的运动时间。
,将P由D点静止释放,求P在斜面上的运动时间。
(2)令 ,在A点给P一个沿斜面上的初速度
,在A点给P一个沿斜面上的初速度 ,求P落地时的动能。
,求P落地时的动能。
(3)将压力传感器X、Y接到同一个数据处理器上,已知当X和Y受到物块压力时,分别显示正值和负值。对于不同的 ,每次都在D点给P一个方向沿斜面向下、大小足够大的初速度,以保证它能滑离斜面。求滑行过程中处理器显示的压力F随
,每次都在D点给P一个方向沿斜面向下、大小足够大的初速度,以保证它能滑离斜面。求滑行过程中处理器显示的压力F随 变化的函数关系式,并在坐标系中画出其函数图象。
变化的函数关系式,并在坐标系中画出其函数图象。
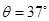 。可视为质点的小物块P(图中未画出)质量m=1kg,它与斜面的动摩擦因数
。可视为质点的小物块P(图中未画出)质量m=1kg,它与斜面的动摩擦因数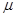 可以通过更换斜面表面的材料进行调节,调节范围是
可以通过更换斜面表面的材料进行调节,调节范围是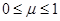 。
。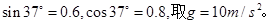

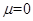 ,将P由D点静止释放,求P在斜面上的运动时间。
,将P由D点静止释放,求P在斜面上的运动时间。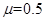 ,在A点给P一个沿斜面上的初速度
,在A点给P一个沿斜面上的初速度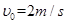 ,求P落地时的动能。
,求P落地时的动能。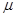 ,每次都在D点给P一个方向沿斜面向下、大小足够大的初速度,以保证它能滑离斜面。求滑行过程中处理器显示的压力F随
,每次都在D点给P一个方向沿斜面向下、大小足够大的初速度,以保证它能滑离斜面。求滑行过程中处理器显示的压力F随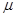 变化的函数关系式,并在坐标系中画出其函数图象。
变化的函数关系式,并在坐标系中画出其函数图象。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com