
题目列表(包括答案和解析)
(12分)1905年爱因斯坦提出了著名的质能关系式:E=mc2,其中E是能量,单位为焦耳(J);m是质量,单位是千克(kg);c为光速,单位是米/秒(m/s),质能关系式说明了质量与能量的对应关系,当质量发生变化时,能量也将发生变化,若质量变化为△ m时,对应的能量变化为 △E,则根据质能关系式有△E =△mc2。
太阳等恒星不断向外辐射能量,是以内部质量的减少为代价的,在太阳内部进行着四个氢核![]() 转变成一个氦核
转变成一个氦核![]() 的核聚变反应,发生核聚变反应时释放出一定的能量,并伴随着一定质量的减少,研究表明,1kg氢聚变时发生的质量减少为7×10-3kg,由于只有太阳核心区的高温才足以使氢核产生聚变反应,所以处于太阳核心区的氢才是可利用的,太阳质量为2.0×1030kg,太阳核心区氢的质量约占太阳质量的十分之一,太阳每秒钟向太空辐射4.0×1026J 能量,问:
的核聚变反应,发生核聚变反应时释放出一定的能量,并伴随着一定质量的减少,研究表明,1kg氢聚变时发生的质量减少为7×10-3kg,由于只有太阳核心区的高温才足以使氢核产生聚变反应,所以处于太阳核心区的氢才是可利用的,太阳质量为2.0×1030kg,太阳核心区氢的质量约占太阳质量的十分之一,太阳每秒钟向太空辐射4.0×1026J 能量,问:
(1)太阳每年因向外辐射能量而减少的质量约为多少千克?
(2)太阳已发光了50亿年,估算太阳还能发光多少年?
(1)有关热辐射和光的本性,请完成下列填空题
黑体辐射的规律不能用经典电磁学理论来解释,1900年德国物理学家普朗克认为能量是由一份一份不可分割最小能量值组成,每一份称为_________.1905年爱因斯坦从此得到启发,提出了光子的观点,认为光子是组成光的最小能量单位,光子的能量表达式为_________,并成功解释了__________________现象中有关极限频率、最大初动能等规律,写出了著名的______________方程,并因此获得诺贝尔物理学奖。
(2)已知氘核质量2.0136u,中子质量为1.0087u,![]() 核质量为3.0150u。
核质量为3.0150u。
A、写出两个氘核聚变成![]() 的核反应方程___________________________________。
的核反应方程___________________________________。
B、计算上述核反应中释放的核能。(结果保留2位有效数字)(1u=931.5Mev)
C、若两氘以相等的动能0.35MeV作对心碰撞即可发生上述核反应,且释放的核能全部转化为机械能,则反应中生成的![]() 核和中子的动能各是多少?(结果保留2位有效数字)
核和中子的动能各是多少?(结果保留2位有效数字)
 核质量为3.0150u。
核质量为3.0150u。 的核反应方程___________________________________。
的核反应方程___________________________________。 核和中子的动能各是多少?(结果保留2位有效数字)
核和中子的动能各是多少?(结果保留2位有效数字)(1)有关热辐射和光的本性,请完成下列填空题。
黑体辐射的规律不能用经典电磁学理论来解释,1900年德国物理学家普朗克认为能量是由一份一份不可分割最小能量值组成,每一份称为_________。1905年爱因斯坦从此得到启发,提出了光子的观点,认为光子是组成光的最小能量单位,光子的能量表达式为_________,并成功解释了_________现象中有关极限频率、最大初动能等规律,写出了著名的_________方程,并因此获得诺贝尔物理学奖。
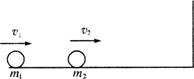
(2)质量分别为m1和m2的两个小球在光滑的水平面上分别以速度v1、v2同向运动并发生对心碰撞,碰后m2被右侧的墙原速弹回,又与m1相碰,碰后两球都静止。求:第一次碰后m1球的速度。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com