练习册

  • 练习册
  • 试题
    7．如图所示.水平地面上停放着A.B两辆小车.质量分别为M和m.M＞m.两车相距为L.人的质量也为m.另有不计质量的一根竹杆和一根细绳.第一次人站在A车上.杆插在B车上.第二次人站在B车上.杆插在A车上.两种情况下.人用同样大小的力拉绳子.使两车相遇.设阻力可忽略不计.两次小车从开始运动到相遇的时间分别为t1和t2.则 ( ) A.t1＞t2 B.t1＜t2 C.t1＝t2 D.条件不足.无法判断 B 解析:当人用力拉绳子时.两小车均做匀加速运动.设人的拉力大小为F. 解法一:当人站在A车拉绳子时.A车的加速度大小为aA=.B车的加速度大小为aB=,设相遇时A车运动的位移大小为.B车的位移大小为则 = aAt12= t12 ------① =aBt12=t22 ------② 而+= --------③ 由①②③得t1= ------④ 当人站要B车上拉绳子时aA=,aB=同理可得 =+= aAt22+ aBt22= t22+ t22 即t2= ------⑤ 比较④⑤,由于M＞m.则M+m＜2M, 知t1＜t2 解法二:第一次人站在A车上拉绳子.设拉力大小为F.则 A车加速度大小 aA=,B车加速度大小 aB= 则A车相对B车加速度大小为 a相＝aA+aB＝+＝ 第二次人站在B车上.拉力大小仍为F.则 A车加速度大小=.B车加速度大小 = 于是A车相对B车加速度大小为=+=+=由于M>m.容易看出a相> 由= a相t12 及 = t22 解得t1＜t2. 解法三:采用极限法分析.由于题设条件M＞m.假设M→∞.则前后两种情况下A车不动.只需考虑B车的运动. 第一次人站在A车上用F力拉绳子.则B车加速度大小为 aB= 第二次人站在B车上用F力拉绳子.则B车加速度大小为 aA= 显然aB > aA.所以t1＜t2. 【查看更多】

     

    题目列表(包括答案和解析)

    如图所示，水平地面上静止放着质量为M，长度为L的厚木板A，A板的右端放有质量为m的物块B（可视为质点）在它们的右端的半截墙上固定着水平放置的弹簧，水平地面P点右侧光滑，左侧粗糙，A与B之间的动摩擦因数为μ，A与P点左侧地面间的动摩擦因数为2μ，让A、B以初速度v0向右匀速运动，B会压缩弹簧，当A的速度减小为零时，B恰好在A的中央处。弹簧将A、B向左弹开的过程中A、B始终具有相同的速度，A、B在P点左侧做匀减速运动，B最后恰好停在A的左端处。问：
    （1）若v0已知，则弹簧被压缩后的最大弹性势能多大？
    （2）试确定v0和板长L应满足的关系式。

    查看答案和解析>>

    如图所示，水平地面上放置一个长木板B，在木板的右端放置着一个质量为m=1kg而大小不计小滑块A，已知B的质量也为m=1kg，A与B之间的动摩擦因数、B与地面之间的动摩擦因数均为μ=0.1，现对B施加一水平恒力F=6N，作用时间t0=1s后撤去F，再过一段时间后A刚好停在B的最左端，则：

    ⑴从A、B刚开始运动到都停下来的过程中摩擦生热是多少？

    ⑵ B的长度是多大？

    查看答案和解析>>

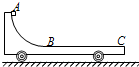    精英家教网如图所示，水平光滑地面上停放着一辆质量为M的小车，其左侧半径为R的四分之一圆弧轨道AB是光滑的，轨道最低点B与水平轨道BC相切，整个轨道处于同一竖直平面内．将质量为m的物块（可视为质点）从A点无初速释放，物块沿轨道滑行至轨道末端C处恰好没有滑出．重力加速度为g，空气阻力可忽略不计．关于物块从A位置运动至C位置的过程，下列说法中正确的是（　　）
    A、小车和物块构成的系统动量守恒
    B、摩擦力对物块和轨道BC所做功的代数和为零
    C、物块的最大速度为
    		2gR
    D、小车的最大速度为
    2m2gR
    M2+Mm

    查看答案和解析>>

    如图所示，一薄木板斜搁在高度一定的平台和水平地板上，其顶端与平台相平，末端置于地板的P处，并与地板平滑连接．将一可看成质点的滑块自木板顶端无初速释放，沿木板下滑，接着在地板上滑动，最终停在Q处．滑块和木板及地板之间的动摩擦因数相同．现将木板截短一半，仍按上述方式搁在该平台和水平地板上，再次将滑块自木板顶端无初速释放，（设物体在板和地面接触处平滑过渡），则滑块最终将停在（　　）

    查看答案和解析>>

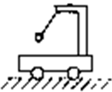    如图所示，光滑水平面上停着一辆小车，小车的固定支架左端用不计质量的细线系一个小铁球．开始将小铁球提起到图示位置，然后无初速释放．不计空气阻力，在小铁球来回摆动的过程中，下列说法正确的是（　　）

    查看答案和解析>>


    同步练习册答案