
题目列表(包括答案和解析)
如图所示,A、B是位于竖直平面内、半径R=0.5m的圆弧形的光滑绝缘轨道,其下端点B与水平绝缘轨道平滑连接,整个轨道处在水平向左的匀强电场中,电场强度E=5×103N/C.今有一质量为m=0.1kg、带电荷量+q=8×10-5C的小滑块(可视为质点)从A点由静止释放.若已知滑块与水平轨道间的动摩擦因数μ=0.05,取g=10m/s2,求:
(1)小滑块第一次经过圆弧形轨道最低点B时对B点的压力.
(2)小滑块在水平轨道上通过的总路程.
|
|
如图所示,A、B是位于竖直平面内、半径R=0.5m的圆弧形的光滑绝缘轨道,其下端点B与水平绝缘轨道平滑连接,整个轨道处在水平向左的匀强电场中,电场强度E=5×103N/C.今有一质量为m=0.1kg、带电荷量+q=8×10-5C的小滑块(可视为质点)从A点由静止释放.若已知滑块与水平轨道间的动摩擦因数μ=0.05,取g=10m/s2,求:
(1)小滑块第一次经过圆弧形轨道最低点B时对B点的压力.
(2)小滑块在水平轨道上通过的总路程.
|
|
 如图所示,A、B是位于竖直平面内、半径R=0.5m的圆弧形的光滑绝缘轨道,其下端点B与水平绝缘轨道平滑连接,整个轨道处在水平向左的匀强电场中,电场强度E=5×103N/C.今有一质量为m=0.1kg、带电荷量+q=8×10-5C的小滑块(可视为质点)从A点由静止释放.若已知滑块与水平轨道间的动摩擦因数μ=0.05,取g=10m/s2,求:
如图所示,A、B是位于竖直平面内、半径R=0.5m的圆弧形的光滑绝缘轨道,其下端点B与水平绝缘轨道平滑连接,整个轨道处在水平向左的匀强电场中,电场强度E=5×103N/C.今有一质量为m=0.1kg、带电荷量+q=8×10-5C的小滑块(可视为质点)从A点由静止释放.若已知滑块与水平轨道间的动摩擦因数μ=0.05,取g=10m/s2,求:
(1)小滑块第一次经过圆弧形轨道最低点B时对B点的压力.
(2)小滑块在水平轨道上通过的总路程.
|
|
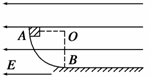 如图所示,A、B是位于竖直平面内、半径R=0.5m的圆弧形的光滑绝缘轨道,其下端点B与水平绝缘轨道平滑连接,整个轨道处在水平向左的匀强电场中,电场强度E=5×103N/C.今有一质量为m=0.1kg、带电荷量+q=8×10-5C的小滑块(可视为质点)从A点由静止释放.若已知滑块与水平轨道间的动摩擦因数μ=0.05,取g=10m/s2,求:
如图所示,A、B是位于竖直平面内、半径R=0.5m的圆弧形的光滑绝缘轨道,其下端点B与水平绝缘轨道平滑连接,整个轨道处在水平向左的匀强电场中,电场强度E=5×103N/C.今有一质量为m=0.1kg、带电荷量+q=8×10-5C的小滑块(可视为质点)从A点由静止释放.若已知滑块与水平轨道间的动摩擦因数μ=0.05,取g=10m/s2,求:
(1)小滑块第一次经过圆弧形轨道最低点B时对B点的压力.
(2)小滑块在水平轨道上通过的总路程.
|
|
如图17所示,固定的凹槽水平表面光滑,其内放置U形滑板N,滑板两端为半径R=0.45m的1/4圆弧面,A和D分别是圆弧的端点,BC段表面粗糙,其余段表面光滑.小滑块P1和P2的质量均为m,滑板的质量M=4m.P1和P2与BC面的动摩擦因数分别为μ1=0.10和μ2=0.40,最大静摩擦力近似等于滑动摩擦力.开始时滑板紧靠槽的左端,P2静止在粗糙面的B点.P1以v0=4.0m/s的初速度从A点沿弧面自由滑下,与P2发生弹性碰撞后,P1处在粗糙面B点上.当P2滑到C点时,滑板恰好与槽的右端碰撞并牢固粘连,P2继续滑动,到达D点时速度为零.P1与P2视为质点,取g=10m/s2,问:
(1)P1在BC段向右滑动时,滑板的加速度为多大?
(2)BC长度为多少?N、P1、P2最终静止后,P1与P2间的距离为多少?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com