
题目列表(包括答案和解析)
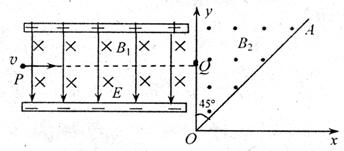
如图所示的平行板器件中,存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1=0.40T,方向垂直于纸面向里,电场强度E=2.0×105V/m,PQ为板间中线,紧靠平行板右侧边缘xoy坐标系的第一象限内,有垂直纸面向外的匀强磁场,磁感应强度B2=0.25T,磁场边界AO和y轴的夹角∠AOy=45°。一束带电荷量q=8.0×10-19C的正粒子从P点射入平行板间,沿中线PQ做直线运动,穿出平行板后从y轴上坐标为(0,0.2m)的Q点垂直y轴射入磁场区域,粒子通过x轴时的速度方向与x轴正方向夹角为45°。不考虑重力的影响。求:
(1)粒子运动的速度![]() 是多大?
是多大?
(2)粒子的质量m是多大?
如图所示,一质量为m,电量为+q的带电粒子从A孔以速度v0垂直AO进入磁感强度为B的匀强磁场中,并恰好从C孔垂直于OC射入匀强电场中,电场方向与OC平行,OC⊥AD,最后打在D点,且![]() =2
=2![]() ,不计重力,求:
,不计重力,求:
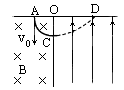
(1)粒子运动到D点所需时间;
(2)粒子抵达D点时的动能.
如图中所示,在真空中坐标xOy平面的x>0的区域内,有磁感应强度![]() 的匀强磁场,方向与xOy平面垂直。在x轴上的P点(10,0)有一放射源,在xOy平面内向各个方向发射速率
的匀强磁场,方向与xOy平面垂直。在x轴上的P点(10,0)有一放射源,在xOy平面内向各个方向发射速率![]() 的带正电的粒子,粒子质量
的带正电的粒子,粒子质量![]() ,粒子带电量
,粒子带电量![]() ,不计重力,试求:
,不计重力,试求:
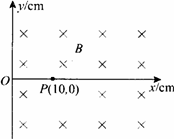
(1)粒子运动的轨道半径和周期;
(2)带电粒子能达到y轴上的范围为多大?
如图所示,一个质量为m、电荷量为+q的带电粒子从A孔以初速度v0垂直AO进入磁感应强度为B的匀强磁场中,并恰好从C孔垂直于OC射入匀强电场中,电场方向跟OC平行,OC⊥AD,最后打在D点,且OD=2OC.若已知m,q,v0,B,不计重力,试求:
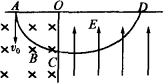
(1)粒子运动到D点所需时间;
(2)粒子抵达D点时的动能.
(14分)
(1)开普勒行星运动第三定律指出:行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比,即![]() ,k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式。已知引力常量为G,太阳的质量为M太。
,k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式。已知引力常量为G,太阳的质量为M太。
(2)开普勒定律不仅适用于太阳系,它对一切具有中心天体的引力系统(如地月系统)都成立。经测定月地距离为3.84×108m,月球绕地球运动的周期为2.36×106S,试计算地球的质M地。(G=6.67×10-11Nm2/kg2,结果保留一位有效数字)
【解析】:(1)因行星绕太阳作匀速圆周运动,于是轨道的半长轴a即为轨道半径r。根据万有引力定律和牛顿第二定律有
![]() ①
①
于是有 ![]() ②
②
即 ![]() ③
③
(2)在月地系统中,设月球绕地球运动的轨道半径为R,周期为T,由②式可得
![]() ④
④
解得 M地=6×1024kg ⑤
(M地=5×1024kg也算对)
23.【题文】(16分)
 如图所示,在以坐标原点O为圆心、半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里。一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从P点射出。
如图所示,在以坐标原点O为圆心、半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里。一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从P点射出。
(1)求电场强度的大小和方向。
(2)若仅撤去磁场,带电粒子仍从O点以相同的速度射入,经![]() 时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
(3)若仅撤去电场,带电粒子仍从O点射入,且速度为原来的4倍,求粒子在磁场中运动的时间。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com