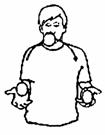
如图5－1－12所示，演员正在进行杂技表演．由图可估算出他将一个鸡蛋抛出的过程中对鸡蛋所做的功最接近于                                              (　　)．

A．0.3 J  　                    B．3 J

C．30 J  　                     D．300 J

如图5－2－9所示，长为L、内壁光滑的直管与水平地面成30°角固定放置．将一质量为m的小球固定在管底，用一轻质光滑细线将小球与质量为M＝km的小物块相连，小物块悬挂于管口．现将小球释放，一段时间后，小物块落地静止不动，小球继续向上运动，通过管口的转向装置后做平抛运动，小球在转向过程中速率不变．(重力加速度为g)．

(1)求小物块下落过程中的加速度大小；

(2)求小球从管口抛出时的速度大小；

(3)试证明小球平抛运动的水平位移总小于L.

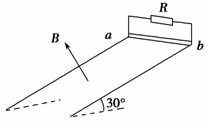
如图9－3－25所示，R₁＝5 Ω，R₂＝6 Ω，电压表与电流表的量程分别为0～10 V和0～3 A，电表均为理想电表．导体棒ab与导轨电阻均不计，且导轨光滑，导轨平面水平，ab棒处于匀强磁场中．

(1)当变阻器R接入电路的阻值调到30 Ω，且用F₁＝40 N的水平拉力向右拉ab棒并使之达到稳定速度v₁时，两表中恰好有一表满偏，而另一表又能安全使用，则此时ab棒的速度v₁是多少？

(2)当变阻器R接入电路的阻值调到3 Ω，且仍使ab棒的速度达到稳定时，两表中恰有一表满偏，而另一表能安全使用，则此时作用于ab棒的水平向右的拉力F₂是多大？

如图9－3－26所示，电阻可忽略的光滑平行金属导轨长s＝1.15 m，两导轨间距L＝0.75 m，导轨倾角为30°，导轨上端ab接一阻值R＝1.5 Ω 的电阻，磁感应强度B＝0.8 T的匀强磁场垂直轨道平面向上．阻值r＝0.5 Ω，质量m＝0.2 kg的金属棒与轨道垂直且接触良好，从轨道上端ab处由静止开始下滑至底端，在此过程中金属棒产生的焦耳热Q₁＝0.1 J．(取g＝10 m/s²)求：

(1)金属棒在此过程中克服安培力的功W_安；

(2)金属棒下滑速度v＝2 m/s时的加速度a.

(3)为求金属棒下滑的最大速度v_m，有同学解答如下：由动能定理，W_重－W_安＝mv，…….由此所得结果是否正确？若正确，说明理由并完成本小题；若不正确，给出正确的解答．

如图3－5－22所示，楔形物体倾角为θ＝30°，放在水平地面上，轻质硬杆下端带有滑轮，上端顶有重1000 N的物体，硬杆只能沿滑槽上下滑动．不计一切摩擦，求作用于楔形物体上的水平推力至少多大才能将重物顶起？

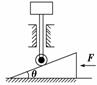
图3－5－22