
题目列表(包括答案和解析)
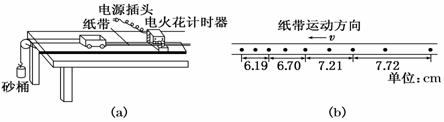
某同学设计了一个探究加速度a与物体所受合力F及质量m关系的实验,图实-4-13(a)所示为实验装置简图.(交流电的频率为50 Hz)
(1)图实-4-13(b)所示为某次实验得到的纸带,根据纸带可求出小车的加速度大小为________m/s2.(保留两位有效数字)
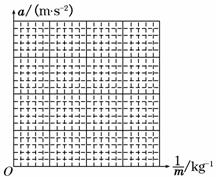
(2)保持砂和砂桶质量不变,改变小车质量m,分别得到小车加速度a与质量m及对应的![]() 数据如下表:
数据如下表:
| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 小车加速度a/m·s-2 | 1.90 | 1.72 | 1.49 | 1.25 | 1.00 | 0.75 | 0.50 | 0.30 |
| 小车质量m/kg | 0.25 | 0.29 | 0.33 | 0.40 | 0.50 | 0.71 | 1.00 | 1.67 |
|
| 4.00 | 3.45 | 3.03 | 2.50 | 2.00 | 1.41 | 1.00 | 0.60 |
请在图实-4-14所示的坐标纸中画出a-![]() 图线,并由图线求出小车加速度a与质量倒数
图线,并由图线求出小车加速度a与质量倒数![]() 之间的关系式是_______________
之间的关系式是_______________
| 实验序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| F/N | 2.42 | 1.90 | 1.43 | 0.97 | 0.76 | 0.50 | 0.23 | 0.06 |
| ω/rad?s-1 | 28.8 | 25.7 | 22.0 | 18.0 | 15.9 | 13.0 | 8.5 | 4.3 |




 在做《研究匀变速直线运动》的实验时,某同学得到一条用打点计时器打下的纸带如图所示,并在其上取了A、B、C、D、E、F、G等7个计数点,每相邻两个计数点之间还有4个点在图中没有画出,打点计时器接周期为T=0.02s的交流电源.经过测量得:d1=3.62cm,d2=8.00cm,d3=13.20cm,d4=19.19cm,d5=25.99cm,d6=33.61cm.
在做《研究匀变速直线运动》的实验时,某同学得到一条用打点计时器打下的纸带如图所示,并在其上取了A、B、C、D、E、F、G等7个计数点,每相邻两个计数点之间还有4个点在图中没有画出,打点计时器接周期为T=0.02s的交流电源.经过测量得:d1=3.62cm,d2=8.00cm,d3=13.20cm,d4=19.19cm,d5=25.99cm,d6=33.61cm.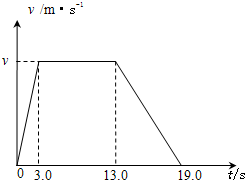 物理兴趣小组活动中,小红提出如下问题:“电梯上升过程中有什么运动规律?”小明同学决定通过实验来探究这一问题.
物理兴趣小组活动中,小红提出如下问题:“电梯上升过程中有什么运动规律?”小明同学决定通过实验来探究这一问题.| 时间(s) | 台秤示数(N) | 钩码超、失重判断 |
| 电梯启动前 | 5.0 | |
| 0~3.0 | 5.8 | |
| 3.0~13.0 | 5.0 | |
| 13.0~19.0 | ? | |
| 19.0以后 | 5.0 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com