
题目列表(包括答案和解析)
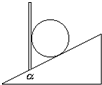 如图所示,在倾角为α的斜面上,一质量为m的小球被竖直的木板挡住,不计一切摩擦,则小球对斜面的压力为( )
如图所示,在倾角为α的斜面上,一质量为m的小球被竖直的木板挡住,不计一切摩擦,则小球对斜面的压力为( ) 如图所示,在倾角为α的斜面上,一质量为m的小球被竖直的木板挡住,不计一切摩擦,则小球对斜面的压力为( )
如图所示,在倾角为α的斜面上,一质量为m的小球被竖直的木板挡住,不计一切摩擦,则小球对斜面的压力为( )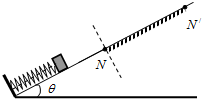 如图所示,在倾角为θ的斜面上,一物块(可视为质点)通过轻绳牵拉压紧弹簧.现将轻绳烧断,物块被弹出,与弹簧分离后即进入足够长的NN′粗糙斜面(虚线下方的摩擦不计),沿斜面上滑达到最远点位置离N距离为S.此后下滑,第一次回到N处,压缩弹簧后又被弹离,第二次上滑最远位置离N距离为
如图所示,在倾角为θ的斜面上,一物块(可视为质点)通过轻绳牵拉压紧弹簧.现将轻绳烧断,物块被弹出,与弹簧分离后即进入足够长的NN′粗糙斜面(虚线下方的摩擦不计),沿斜面上滑达到最远点位置离N距离为S.此后下滑,第一次回到N处,压缩弹簧后又被弹离,第二次上滑最远位置离N距离为| S | 2 |
如图所示,在倾角为θ的斜面上,一物块(可视为质点)通过轻绳牵拉压紧弹簧.现将轻绳烧断,物块被弹出,与弹簧分离后即进入足够长的N N / 粗糙斜面(虚线下方的摩擦不计),沿斜面上滑达到最远点位置离N距离为S.此后下滑,第一次回到N处,压缩弹簧后又被弹离,第二次上滑最远位置离N距离为S/2.求:物块与粗糙斜面间N N /段的动摩擦因数
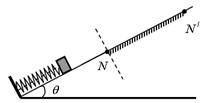
(8分)如图所示,在倾角为θ的斜面上,一物块(可视为质点)通过轻绳牵拉压紧弹簧.现将轻绳烧断,物块被弹出,与弹簧分离后即进入足够长的N N / 粗糙斜面(虚线下方的摩擦不计),沿斜面上滑达到最远点位置离N距离为S.此后下滑,第一次回到N处,压缩弹簧后又被弹离,第二次上滑最远位置离N距离为S/2.求:物块与粗糙斜面间N N /段的动摩擦因数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com