如图甲所示,长方形金属框abcd(下面简称方框),各边长度为ac=bd=
、ab=cd=l,方框外侧套着一个内侧壁长分别为
及l的U型金属框架MNPQ(下面简称U型框),U型框与方框之间接触良好且无摩擦.两个金属框的质量均为m,PQ边、ab边和cd边的电阻均为r,其余各边电阻可忽略不计.将两个金属框放在静止在水平地面上的矩形粗糙绝缘平面上,将平面的一端缓慢抬起,直到这两个金属框都恰能在此平面上匀速下滑,这时平面与地面的夹角为θ,此时将平面固定构成一个倾角为θ的斜面.已知两框与斜面间的最大静摩擦力近似等于滑动摩擦力.在斜面上有两条与其底边垂直的、电阻可忽略不计,且足够长的光滑金属轨道,两轨道间的宽度略大于l,使两轨道能与U型框保持良好接触,在轨道上端接有电压传感器并与计算机相连,如图乙所示.在轨道所在空间存在垂直于轨道平面斜向下、磁感强度大小为B的匀强磁场.
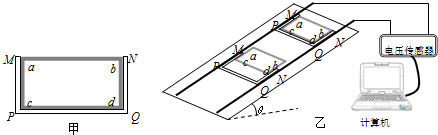
(1)若将方框固定不动,用与斜面平行,且垂直PQ边向下的力拉动U型框,使它匀速向下运动,在U形框与方框分离之前,计算机上显示的电压为恒定电压U
0,求U型框向下运动的速度多大;
(2)若方框开始时静止但不固定在斜面上,给U型框垂直PQ边沿斜面向下的初速度v
0,如果U型框与方框最后能不分离而一起运动,求在这一过程中电流通过方框产生的焦耳热;
(3)若方框开始时静止但不固定在斜面上,给U型框垂直PQ边沿斜面向下的初速度3v
0,U型框与方框将会分离.求在二者分离之前U型框速度减小到2v
0时,方框的加速度.
注:两个电动势均为E、内阻均为r的直流电源,若并联在一起,可等效为电动势仍为E,内电阻为
的电源;若串联在一起,可等效为电动势为2E,内电阻为2r的电源.


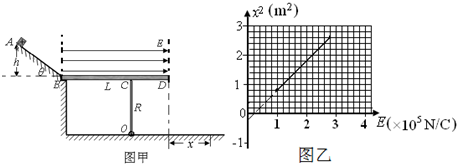
 如图甲所示,一个绝缘倾斜直轨道固定在竖直面内,轨道的AB部分粗糙,BF部分光滑.整个空间存在着竖直方向的周期性变化的匀强电场,电场强度随时间的变化规律如图乙所示,t=0时电场方向竖直向下.在虚线的右侧存在着垂直纸面向里的匀强磁场,磁感应强度为B=
如图甲所示,一个绝缘倾斜直轨道固定在竖直面内,轨道的AB部分粗糙,BF部分光滑.整个空间存在着竖直方向的周期性变化的匀强电场,电场强度随时间的变化规律如图乙所示,t=0时电场方向竖直向下.在虚线的右侧存在着垂直纸面向里的匀强磁场,磁感应强度为B=