用落体法“验证机械能守恒定律”的实验中：(g取9.8 m/s²)

(1)运用公式mv²＝mgh时对实验条件的要求是________________．为此目的，所选择的纸带第1、2两点间的距离应接近__________．

(2)若实验中所用重物质量m＝1 kg，打点纸带如图所示，打点时间间隔为0.02 s，则记录B点时，重物速度v_B＝________，重物动能E_k＝________；从开始下落起至B点，重物的重力势能减小量是__________，由此可得出的结论是____________________________________．

 (3)根据纸带算出各点的速度v，量出下落距离h，则以为纵轴，以h为横轴画出的图象应是图中的                                             (　　)

【解析】：(1)自由下落的物体在第一个0.02 s内，下落距离

h＝gt²＝2 mm

(2)v_B＝＝ m/s＝0.59 m/s

E_k＝mv_B²＝×1×0.59² J≈0.174 J

ΔE_p＝mgh＝1×9.8×17.9×10^－3 J≈0.175 J.

解析　(1)设木板第一次上升过程中，物块的加速度为a_物块，由牛顿第二定律kmgsin θ－mgsin θ＝ma_物块

解得a_物块＝(k－1)gsin θ，方向沿斜面向上

(2)设以地面为零势能面，木板第一次与挡板碰撞时的速度大小为v₁

由机械能守恒得：×2mv＝2mgH

解得v₁＝

设木板弹起后的加速度为a_板，由牛顿第二定律得：

a_板＝－(k＋1)gsin θ

木板第一次弹起的最大路程s₁＝＝

木板运动的路程s＝＋2s₁＝

(3)设物块相对木板滑动距离为L

根据能量守恒mgH＋mg(H＋Lsin θ)＝kmgLsin θ

摩擦力对木板及物块做的总功W＝－kmgLsin θ

解得W＝－

答案　(1)(k－1)gsin θ；方向沿斜面向上

(2)　(3)－

光电计时器是物理实验中经常用到的一种精密计时仪器，它由光电门和计时器两部分组成，光电门的一臂的内侧附有发光装置(发射激光的装置是激光二极管，发出的光束很细)，如图中的A和A′，另一臂的内侧附有接收激光的装置，如图实－4－12中的B和B′，当物体在它们之间通过时，二极管发出的激光被物体挡住，接收装置不能接

收到激光信号，同时计时器就开始计时，直到挡光结束光电计时器停止计时，故此装置能精确地记录物体通过光电门所用的时间．现有一小球从两光电门的正上方开始自由下落，如图所示．

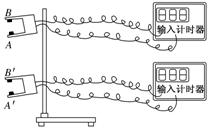
 (1)若要用这套装置来验证机械能守恒定律，则要测量的物理量有________________________(每个物理量均用文字和字母表示，如高度H)．

(2)验证机械能守恒定律的关系式为________．

【解析】：本实验是围绕机械能守恒定律的验证设计的，关键是速度的测定，本题改打点计时器测量速度为光电门测量．由于本装置可记录小球通过光电门的时间Δt，则将小球的直径D除以Δt，即可求出小球经过光电门的速度，若再测出两光电门间相距的高度H，即可验证机械能守恒定律．

(1)需要测量的物理量有：小球直径D，两光电门间的竖直高度H，小球通过上、下两光电门的时间Δt₁、Δt₂.则小球通过上、下两光电门处的速度分别为、.

(2)验证守恒关系式为：

m()²－m()²＝mgH，

化简得：－＝2gH.

解析　(1)小球从曲面上滑下，只有重力做功，由机械能守恒定律知：

mgh＝mv                                                       ①

得v₀＝＝ m/s＝2 m/s.

(2)小球离开平台后做平抛运动，小球正好落在木板的末端，则

H＝gt²                                                                                                                                                      ②

＝v₁t                                                                                                                ③

联立②③两式得：v₁＝4 m/s

设释放小球的高度为h₁，则由mgh₁＝mv

得h₁＝＝0.8 m.

(3)由机械能守恒定律可得：mgh＝mv²

小球由离开平台后做平抛运动，可看做水平方向的匀速直线运动和竖直方向的自由落体运动，则：

y＝gt²                                                                                                                                                       ④

x＝vt                                                                                                                       ⑤

tan 37°＝                                                                                                          ⑥

v_y＝gt                                                                                                                      ⑦

v＝v²＋v                                                       ⑧

E_k＝mv                                                      ⑨

由④⑤⑥⑦⑧⑨式得：E_k＝32.5h                                                                       ⑩

考虑到当h>0.8 m时小球不会落到斜面上，其图象如图所示

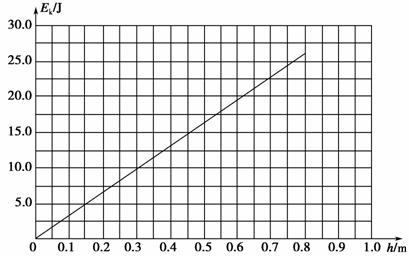
答案　(1)2 m/s　(2)0.8 m　(3)E_k＝32.5h　图象见解析

光电计时器是物理实验中经常用到的一种精密计时仪器，它由光电门和计时器两部分组成，光电门的一臂的内侧附有发光装置(发射激光的装置是激光二极管，发出的光束很细)，如图中的A和A′，另一臂的内侧附有接收激光的装置，如图实－4－12中的B和B′，当物体在它们之间通过时，二极管发出的激光被物体挡住，接收装置不能接

收到激光信号，同时计时器就开始计时，直到挡光结束光电计时器停止计时，故此装置能精确地记录物体通过光电门所用的时间．现有一小球从两光电门的正上方开始自由下落，如图所示．

 (1)若要用这套装置来验证机械能守恒定律，则要测量的物理量有________________________(每个物理量均用文字和字母表示，如高度H)．

(2)验证机械能守恒定律的关系式为________．

【解析】：本实验是围绕机械能守恒定律的验证设计的，关键是速度的测定，本题改打点计时器测量速度为光电门测量．由于本装置可记录小球通过光电门的时间Δt，则将小球的直径D除以Δt，即可求出小球经过光电门的速度，若再测出两光电门间相距的高度H，即可验证机械能守恒定律．

(1)需要测量的物理量有：小球直径D，两光电门间的竖直高度H，小球通过上、下两光电门的时间Δt₁、Δt₂.则小球通过上、下两光电门处的速度分别为、.

(2)验证守恒关系式为：

m()²－m()²＝mgH，

化简得：－＝2gH.