
题目列表(包括答案和解析)
| 1 |
| 4 |
| 1 |
| 2 |
| v | 2 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| v | 2 1 |
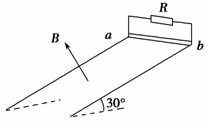
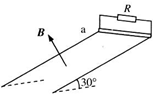
 (2011?上海)电阻可忽略的光滑平行金属导轨长S=1.15m,两导轨间距L=0.75m,导轨倾角为30°,导轨上端ab接一阻值R=1.5Ω的电阻,磁感应强度B=0.8T的匀强磁场垂直轨道平面向上.阻值r=0.5Ω,质量m=0.2kg的金属棒与轨道垂直且接触良好,从轨道上端ab处由静止开始下滑至底端,在此过程中金属棒产生的焦耳热Qr=0.1J.(取g=10m/s2)求:
(2011?上海)电阻可忽略的光滑平行金属导轨长S=1.15m,两导轨间距L=0.75m,导轨倾角为30°,导轨上端ab接一阻值R=1.5Ω的电阻,磁感应强度B=0.8T的匀强磁场垂直轨道平面向上.阻值r=0.5Ω,质量m=0.2kg的金属棒与轨道垂直且接触良好,从轨道上端ab处由静止开始下滑至底端,在此过程中金属棒产生的焦耳热Qr=0.1J.(取g=10m/s2)求:| 1 | 2 |
如图9-3-26所示,电阻可忽略的光滑平行金属导轨长s=1.15 m,两导轨间距L=0.75 m,导轨倾角为30°,导轨上端ab接一阻值R=1.5 Ω 的电阻,磁感应强度B=0.8 T的匀强磁场垂直轨道平面向上.阻值r=0.5 Ω,质量m=0.2 kg的金属棒与轨道垂直且接触良好,从轨道上端ab处由静止开始下滑至底端,在此过程中金属棒产生的焦耳热Q1=0.1 J.(取g=10 m/s2)求:
(1)金属棒在此过程中克服安培力的功W安;
(2)金属棒下滑速度v=2 m/s时的加速度a.
(3)为求金属棒下滑的最大速度vm,有同学解答如下:由动能定理,W重-W安=![]() mv
mv![]() ,…….由此所得结果是否正确?若正确,说明理由并完成本小题;若不正确,给出正确的解答.
,…….由此所得结果是否正确?若正确,说明理由并完成本小题;若不正确,给出正确的解答.
![]()
| 1 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com