
题目列表(包括答案和解析)
| U2R2-U1R1 |
| U1-U2 |
| U2R2-U1R1 |
| U1-U2 |
| 实验次数i | Fi(N) | Li(cm) |
| 1 | 0.49 | 60.20 |
| 2 | 0.98 | 61.60 |
| 3 | 1.47 | 63.05 |
| 4 | 1.96 | 64.65 |
| 5 | 2.45 | 66.10 |
| 6 | 2.94 | 67.55 |
. |
| △L |
| (L2-L1)+(L3-L2)+…(L6-L5) |
| 5 |
| L6-L5 |
| 5 |
| 67.55-60.20 |
| 5 |
| △F |
| △L |
| 0.49N |
| 1.47cm |
 的刻度盘只标注了表示量程Ig=100μA的刻度线,尚未标注其他分刻度线,如图所2示.请用下列全部器材测量微安表
的刻度盘只标注了表示量程Ig=100μA的刻度线,尚未标注其他分刻度线,如图所2示.请用下列全部器材测量微安表 的内阻:
的内阻: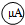 :内阻Rg约为2kΩ
:内阻Rg约为2kΩ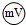 :量程250mV,最小分度5mV,内阻约为1kΩ
:量程250mV,最小分度5mV,内阻约为1kΩ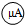 的内阻Rg的实验电路原理图(原理图中的元①要用相应的英文字母标注).
的内阻Rg的实验电路原理图(原理图中的元①要用相应的英文字母标注).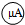 的内阻Rg=
的内阻Rg=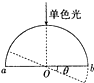 如图所示,一束单无双光沿折射率为n的半圆柱形玻璃砖的半径垂直ab面入射,有光线从ab面射出.以O点为圆心,将玻璃砖缓慢转过θ角时,恰好没有光线从ab面射出.则θ为(反三角函数表示法:例,sinθ=A,则θ=sin-1 A)( )
如图所示,一束单无双光沿折射率为n的半圆柱形玻璃砖的半径垂直ab面入射,有光线从ab面射出.以O点为圆心,将玻璃砖缓慢转过θ角时,恰好没有光线从ab面射出.则θ为(反三角函数表示法:例,sinθ=A,则θ=sin-1 A)( )(20分)惰性气体分子为单原子分子,在自由原子情形下,其电子电荷分布是球对称的。负电荷中心与原子核重合。但如两个原子接近,则彼此能因静电作用产生极化(正负电荷中心不重合),从而导致有相互作用力,这称为范德瓦尔斯相互作用。下面我们采用一种简化模型来研究此问题。
当负电中心与原子核不重合时,若以x表示负电中心相对正电荷(原子核)的位移,当x为正时,负电中心在正电荷的右侧,当x为负时,负电中心在正电荷的左侧,如图1所示。这时,原子核的正电荷对荷外负电荷的作用力f相当于一个劲度系数为k的弹簧的弹性力,即f=-kx,力的方向指向原子核,核外负电荷的质量全部集中在负电中心,此原子可用一弹簧振子来模拟。
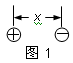
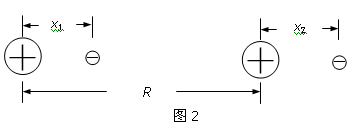
今有两个相同的惰性气体原子,它们的原子核固定,相距为R,原子核正电荷的电荷量为q,核外负电荷的质量为m。因原子间的静电相互作用,负电中心相对各自原子核的位移分别为x1和x2,且|x1|和|x2|都远小于R,如图2所示。此时每个原子的负电荷除受到自己核的正电荷作用外,还受到另一原子的正、负电荷的作用。
众所周知,孤立谐振子的能量E=![]() mv2+
mv2+![]() kx2是守恒的,式中v为质量m的振子运动的速度,x为振子相对平衡位置的位移。量子力学证明,在绝对零度时,谐振子的能量为
kx2是守恒的,式中v为质量m的振子运动的速度,x为振子相对平衡位置的位移。量子力学证明,在绝对零度时,谐振子的能量为![]() hω,称为零点振动能,
hω,称为零点振动能,![]() ,h为普朗克常量,
,h为普朗克常量,![]() 为振子的固有角频率。试计算在绝对零度时上述两个有范德瓦尔斯相互作用的惰性气体原子构成的体系的能量,与两个相距足够远的(可视为孤立的、没有范德瓦尔斯相互作用的)惰性气体原子的能量差,并从结果判定范德瓦尔斯相互作用是吸引还是排斥。可利用当|x|<<1时的近似式
为振子的固有角频率。试计算在绝对零度时上述两个有范德瓦尔斯相互作用的惰性气体原子构成的体系的能量,与两个相距足够远的(可视为孤立的、没有范德瓦尔斯相互作用的)惰性气体原子的能量差,并从结果判定范德瓦尔斯相互作用是吸引还是排斥。可利用当|x|<<1时的近似式![]() ≈1+
≈1+![]() x-
x-![]() x2,(1+x)-1≈1-x+x2。
x2,(1+x)-1≈1-x+x2。
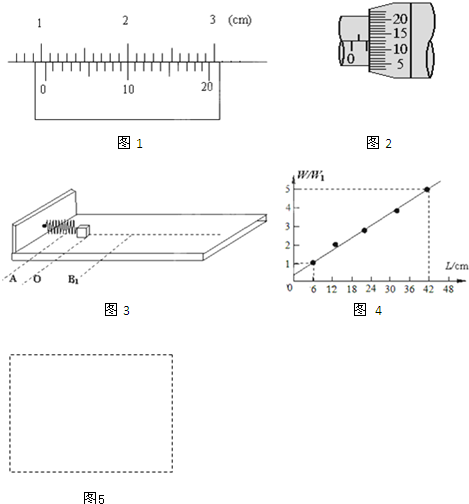
(分)(1)某实验小组用如图所示的装置测量弹簧的劲度系数k。当挂在弹簧下端的砝码处于静止状态时,测出弹簧受到的拉力F与对应的弹簧长度L(弹簧始终在弹性限度内),列表记录如下:
| 实验次数i | Fi(N) | Li(cm) |
| 1 | 0.49 | 60.20 |
| 2 | 0.98 | 61.60 |
| 3 | 1.47 | 63.05 |
| 4 | 1.96 | 64.65 |
| 5 | 2.45 | 66.10 |
| 6 | 2.94 | 67.55 |

因为逐差法常用于处理自变量等间距变化的数据组,所以小组一成员用逐差法处理数据,具体如下:将表中第三列相邻的两项求差,得出弹簧伸长量ΔL= Li - Li-1
每个ΔL都是与相同的拉力ΔF=0.49N相对应的伸长量,求出ΔL的平均值
===cm=1.47cm
故该弹簧的劲度系数为k===0.333N/cm
该成员在实验数据处理中存在的问题是: ;
请你用逐差法处理表格中的数据,尽量精确计算出弹簧的劲度系数k= N/cm(结果保留三位有效数字)。
 (2)一微安表
(2)一微安表![]() 的刻度盘只标注了表示量程Ig =100μA的刻度线,尚未标注其他分刻度线,如图所示。请用下列全部器材测量微安表
的刻度盘只标注了表示量程Ig =100μA的刻度线,尚未标注其他分刻度线,如图所示。请用下列全部器材测量微安表![]() 的内阻:
的内阻:
i、图示的待测微安表![]() :内阻Rg约为2kΩ
:内阻Rg约为2kΩ
ii、1块毫伏表![]() :量程250mV,最小分度5mV,内阻约为1kΩ
:量程250mV,最小分度5mV,内阻约为1kΩ
iii、1个滑动变阻器R1:0~50Ω
 iv、1个滑动变阻器R2:0~3kΩ
iv、1个滑动变阻器R2:0~3kΩ
v、1个直流电源E:电动势E=1.5V,内阻r约为1Ω
vi、1个单刀单掷开关S,导线若干
①在方框内画出测量微安表![]() 的内阻Rg的实验电路原理图(原理图中的元件要用相应的英文字母标注)。
的内阻Rg的实验电路原理图(原理图中的元件要用相应的英文字母标注)。
②下面是主要的实验操作步骤,将所缺的内容填写在横线上方:
第一步:断开S,按电路原理图连接器材,将两个滑动变阻器 R1、R2的触头分别置于合理的位置;
第二步:闭合S,分别调节R1和R2至适当位置,
③用已知量和测得量的符号表示微安表![]() 的内阻Rg=
的内阻Rg=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com