
题目列表(包括答案和解析)
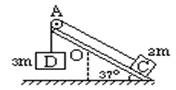 质量为2m长为L的均匀木板AB,如图所示,安装在光滑轴O上,并可绕轴O在竖直平面内转动,木板静止时与水平面间夹角37°,质量为2m的物体C放在木板B端,并用绕过木板A滑轮的绳子与质量为3m的物体D连接,若物体C与木板间的动摩擦因数μ为0.5,OA长为0.4L,求物体C由静止开始运动到距B端多远处时,木板开始转动,(滑轮绳子质量及摩擦均不计)(sin37°=0.6.cos37°=0.8.g=10m/
质量为2m长为L的均匀木板AB,如图所示,安装在光滑轴O上,并可绕轴O在竖直平面内转动,木板静止时与水平面间夹角37°,质量为2m的物体C放在木板B端,并用绕过木板A滑轮的绳子与质量为3m的物体D连接,若物体C与木板间的动摩擦因数μ为0.5,OA长为0.4L,求物体C由静止开始运动到距B端多远处时,木板开始转动,(滑轮绳子质量及摩擦均不计)(sin37°=0.6.cos37°=0.8.g=10m/![]() )
)
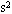 )
)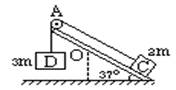

图1-8-5
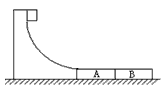
如图1-8-5所示,两个完全相同的质量为m的木板A、B置于水平地面上,它们的间距s=2.88 m.质量为2m、大小可忽略的物块C置于A板的左端.C与A之间的动摩擦因数为μ1=0.22,A、B与水平地面之间的动摩擦因数为μ2=0.10,最大静摩擦力可认为等于滑动摩擦力.开始时,三个物体处于静止状态.现给C施加一个水平向右、大小为![]() mg的恒力F,假定木板A、B碰撞时间极短且碰撞后黏连在一起.要使C最终不脱离木板,每块木板的长度至少应为多少?
mg的恒力F,假定木板A、B碰撞时间极短且碰撞后黏连在一起.要使C最终不脱离木板,每块木板的长度至少应为多少?
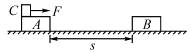
图1-8-5
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com