
题目列表(包括答案和解析)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
银河系的恒量中大约有四分之一是双星,某双星由质量不等的星体S1和S2构成,两星在相互之间的万有引力作用下绕两者连线某一点C做匀速圆周运动,已知S1和S2的质量分别为M1和M2,S1和S2的距离为L,已知引力常数为G。由此可求出S1的角速度为( )(A) (B)
(B)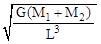 (C)
(C)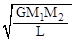 (D)
(D)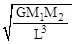
银河系的恒量中大约有四分之一是双星,某双星由质量不等的星体S1和S2构成,两星在相互之间的万有引力作用下绕两者连线某一点C做匀速圆周运动,已知S1和S2的质量分别为M1和M2,S1和S2的距离为L,已知引力常数为G。由此可求出S1的角速度为( )
A.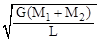 B.
B.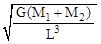 C.
C. D.
D.
A.
| B.
| C.
| D.
|
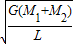
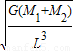
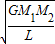
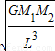
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com