
题目列表(包括答案和解析)
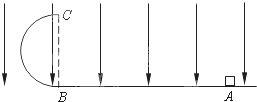 如图所示,竖直放置的半圆形绝缘光滑轨道半径R=40cm,下端与绝缘光滑的水平面平滑连接,整个装置处于方向竖直向下,大小为E=1×103V/m的匀强电场中,一质量为m=10g、带电量为q=+1×10-4C的小物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好能通过最高点C,取g=10m/s2,试求:
如图所示,竖直放置的半圆形绝缘光滑轨道半径R=40cm,下端与绝缘光滑的水平面平滑连接,整个装置处于方向竖直向下,大小为E=1×103V/m的匀强电场中,一质量为m=10g、带电量为q=+1×10-4C的小物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好能通过最高点C,取g=10m/s2,试求: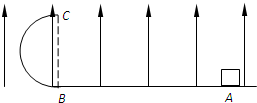 如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场E中.一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好通过最高点C,场强大小E<
如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场E中.一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好通过最高点C,场强大小E<| mg | q |
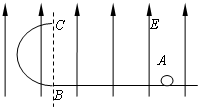
 如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与光滑绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场中E中,一质量为m带电量+q的物块(可视为质点),从水平面上的A占以初速度v0水平向左运动沿半圆形轨道恰好通过最高点C,场强大小为E(E<mg/q)
如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与光滑绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场中E中,一质量为m带电量+q的物块(可视为质点),从水平面上的A占以初速度v0水平向左运动沿半圆形轨道恰好通过最高点C,场强大小为E(E<mg/q) 如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场E中.一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好通过最高点C,场强大小E<
如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场E中.一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好通过最高点C,场强大小E<| mg | q |
| mg |
| q |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com