
题目列表(包括答案和解析)
有两个完全相同的小滑块A和B,A沿光滑水平面以速度v0与静止在平面边缘O点的B发生正碰,碰撞中无机械能损失。碰后B运动的轨迹为OD曲线,如图所示。(1)已知滑块质量为m,碰撞时间为![]() ,求碰撞过程中A对B平均冲力的大小。(2)为了研究物体从光滑抛物线轨道顶端无初速下滑的运动,特制做一个与B平抛轨道完全相同的光滑轨道,并将该轨道固定在与OD曲线重合的位置,让A沿该轨道无初速下滑(经分析,A下滑过程中不会脱离轨道)。
,求碰撞过程中A对B平均冲力的大小。(2)为了研究物体从光滑抛物线轨道顶端无初速下滑的运动,特制做一个与B平抛轨道完全相同的光滑轨道,并将该轨道固定在与OD曲线重合的位置,让A沿该轨道无初速下滑(经分析,A下滑过程中不会脱离轨道)。
a.分析A沿轨道下滑到任意一点的动量pA与B平抛经过该点的动量pB的大小关系;
b.在OD曲线上有一M点,O和M两点连线与竖直方向的夹角为45°。求A通过M点时的水平分速度和竖直分速度。
有两个完全相同的小滑块A和B,A沿光滑水平面以速度v0与静止在平面边缘O点的B发生正碰,碰撞中无机械能损失。碰后B运动的轨迹为OD曲线,如图所示。
(1)已知滑块质量为m,碰撞时间为![]() ,求碰撞过程中A对B平均冲力的大小。
,求碰撞过程中A对B平均冲力的大小。
(2)为了研究物体从光滑抛物线轨道顶端无初速下滑的运动,特制做一个与B平抛轨道完全相同的光滑轨道,并将该轨道固定在与OD曲线重合的位置,让A沿该轨道无初速下滑(经分析,A下滑过程中不会脱离轨道)。
a.分析A沿轨道下滑到任意一点的动量pA与B平抛经过该点的动量pB的大小关系;
b.在OD曲线上有一M点,O和M两点连线与竖直方向的夹角为45°。求A通过M点时的水平分速度和竖直分速度。

(16分)
有两个完全相同的小滑块A和B,A沿光滑水平面以速度v0与静止在平面边缘O点的B发生正碰,碰撞中无机械能损失。碰后B运动的轨迹为OD曲线,如图所示。
(1)已知滑块质量为m,碰撞时间为,求碰撞过程中A对B平均冲力的大小。
(2)为了研究物体从光滑抛物线轨道顶端无初速下滑的运动,特制做一个与B平抛轨道完全相同的光滑轨道,并将该轨道固定在与OD曲线重合的位置,让A沿该轨道无初速下滑(经分析,A下滑过程中不会脱离轨道)。
a.分析A沿轨道下滑到任意一点的动量pA与B平抛经过该点的动量pB的大小关系;
b.在OD曲线上有一M点,O和M两点连线与竖直方向的夹角为45°。求A通过M点时的水平分速度和竖直分速度。
(16分)
有两个完全相同的小滑块A和B,A沿光滑水平面以速度v0与静止在平面边缘O点的B发生正碰,碰撞中无机械能损失。碰后B运动的轨迹为OD曲线,如图所示。
(1)已知滑块质量为m,碰撞时间为 ,求碰撞过程中A对B平均冲力的大小。
,求碰撞过程中A对B平均冲力的大小。
(2)为了研究物体从光滑抛物线轨道顶端无初速下滑的运动,特制做一个与B平抛轨道完全相同的光滑轨道,并将该轨道固定在与OD曲线重合的位置,让A沿该轨道无初速下滑(经分析,A下滑过程中不会脱离轨道)。
a.分析A沿轨道下滑到任意一点的动量pA与B平抛经过该点的动量pB的大小关系;
b.在OD曲线上有一M点,O和M两点连线与竖直方向的夹角为45°。求A通过M点时的水平分速度和竖直分速度。
(16分)
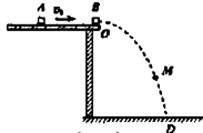
有两个完全相同的小滑块A和B,A沿光滑水平面以速度v0与静止在平面边缘O点的B发生正碰,碰撞中无机械能损失。碰后B运动的轨迹为OD曲线,如图所示。
(1)已知滑块质量为m,碰撞时间为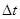 ,求碰撞过程中A对B平均冲力的大小。
,求碰撞过程中A对B平均冲力的大小。
(2)为了研究物体从光滑抛物线轨道顶端无初速下滑的运动,特制做一个与B平抛轨道完全相同的光滑轨道,并将该轨道固定在与OD曲线重合的位置,让A沿该轨道无初速下滑(经分析,A下滑过程中不会脱离轨道)。
a.分析A沿轨道下滑到任意一点的动量pA与B平抛经过该点的动量pB的大小关系;
b.在OD曲线上有一M点,O和M两点连线与竖直方向的夹角为45°。求A通过M点时的水平分速度和竖直分速度。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com