如图甲所示,光滑绝缘斜面AB,高h=0.1m,底端B与一块质量为M=2kg的均匀、水平放置的绝缘平板光滑连接,平板长为L=1m,其距B端0.6m处C固定在高为R=0.5m的竖直支架上,支架的下端与垂直于纸面的固定转轴O连接,平板可绕转轴O沿顺时针方向翻转,在支架正上方有一个水平向右的有界匀强电场E.在斜面顶端A放置带正电q=1×10
-5C的很小的物体,质量为m,使其由静止滑下,沿平板进入电场,能滑过D点,并从D点飞出到水平地面上,设物体从D点飞出的水平距离为x,如图乙是x
2与E图象,重力加速度g取10m/s
2.问:
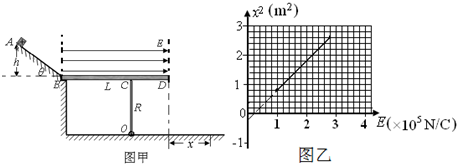
(1)图乙中物体的质量m为多大?物体与平板间的动摩擦因数μ是多大?
(2)为保证不同质量物体都能滑过D点,且平板不翻转,求物体的质量的取值范围?
(3)为保证不同质量物体都能滑过D点,且平板不翻转,求水平匀强电场E的大小范围?
(4)平板出现漏电是常有的事情(漏电不影响电场分布),假设图乙中物体m的带电减少量△q随在平板上滑过的长度成正比,即△q=ks(k=5×10
-6C/m),为保证物体滑到D点并且飞出的水平距离为1m,求此时匀强电场E的大小;请在图乙中画出平板漏电情况下的x
2与E图象.




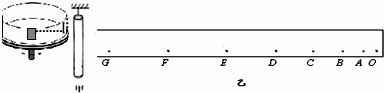
 25.如图甲所示,光滑、绝缘直角三角型斜面
25.如图甲所示,光滑、绝缘直角三角型斜面![]() 固定在水平地面上,
固定在水平地面上,![]() 边长
边长![]() ;虚线左、右空间存在
;虚线左、右空间存在![]()
![]() 的匀强磁场,方向分别垂直于纸面向里、向外;整个空间存在着竖直方向的、随时问交替变化的匀强电场(如图乙所示,竖直向上方向为正方向)。在距
的匀强磁场,方向分别垂直于纸面向里、向外;整个空间存在着竖直方向的、随时问交替变化的匀强电场(如图乙所示,竖直向上方向为正方向)。在距![]() 点
点![]() 处的
处的![]() 点有一物块抛射器,在
点有一物块抛射器,在![]() 时刻将一质量为
时刻将一质量为![]() 、带电荷量为
、带电荷量为![]() 的小物块(可视为质点)抛入电磁场,小物块恰好能在
的小物块(可视为质点)抛入电磁场,小物块恰好能在![]() 点切入
点切入![]() 斜面。设小物块在
斜面。设小物块在![]() 面上滑行时无电荷损失且所受洛伦兹力小于
面上滑行时无电荷损失且所受洛伦兹力小于![]() ,求:
,求:![]() 点所用时间。
点所用时间。