
题目列表(包括答案和解析)
甲车以加速度3 m/s2由静止开始作匀加速直线运动,乙车落后2秒在同一地点由静止开始,以加速度4 m/s2作匀加速直线运动,两车的运动方向相同,求:
(1)在乙车追上甲车之前,两车距离的最大值是多少?
(2)乙车出发后经多长时间可追上甲车?此时它们离开出发点多远?
甲车以加速度3 m/s2由静止开始作匀加速直线运动,乙车落后2 s钟在同一地点由静止开始,以加速度4 m/s2作匀加速直线运动,两车的运动方向相同,求:
(1)在乙车追上甲车之前,两车距离的最大值是多少?
(2)乙车出发后经多长时间可追上甲车?此时它们离开出发点多远?
甲车以加速度3 m/s2由静止开始作匀加速直线运动,乙车落后2 s钟在同一地点由静止开始,以加速度4 m/s2作匀加速直线运动,两车的运动方向相同,求:
(1)在乙车追上甲车之前,两车距离的最大值是多少?
(2)乙车出发后经多长时间可追上甲车?此时它们离开出发点多远?
甲车以加速度3 m/s2由静止开始作匀加速直线运动,乙车落后2 s钟在同一地点由静止开始,以加速度4 m/s2作匀加速直线运动,两车的运动方向相同,求:在乙车追上甲车之前,两车距离的最大值是多少?
某同学在“验证牛顿第二定律的实验”中,所用实验装置如右图甲所示,打点计时器接频率为50Hz的交流电源.开始实验时, 在细线末端挂上适当的钩码;由静止起释放小车后,小车在水平长木板上向左做匀加速运动,与小车相连接的纸带上被打出一系列的点.
⑴右图乙给出的是该同学在实验中获取的一条纸带的一部分,其中1、2、3、4是选取的计数点,相邻两计数点间还有4个点,计数点间的距离如图所示.根据图乙中所标数据可计算得小车运动的加速度a= m/s2,与计数点2对应的小车瞬时速度大小v2= m/s.
(以上结果均保留2位有效数字)


⑵实验中,该同学测出所挂钩码重力F并以此作为小车运动时细线的拉力,事先还测得小车的质量M,而后他根据公式 计算出小车运动的加速度a.他发现在绝大多数情况下,根据上述公式计算出的加速度值要比利用纸带测出的加速度值大.若该同学在实验操作过程中没有其他错误,试分析其中的两点主要原因:①
计算出小车运动的加速度a.他发现在绝大多数情况下,根据上述公式计算出的加速度值要比利用纸带测出的加速度值大.若该同学在实验操作过程中没有其他错误,试分析其中的两点主要原因:①
 ;②
.
;②
.
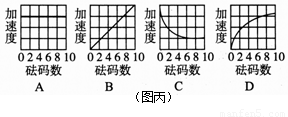
⑶另一个同学在完成同样的实验时,在细线末端逐次增加一个质量m0=50g的钩码,然后利用纸带测出每次小车运动的加速度.如果小车质量M=100g,细线质量忽略不计,那么右图丙中最适合用来描述小车加速度随着所挂钩码个数而变化的图线是 .

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com