
题目列表(包括答案和解析)
(12分)如右图,半径为R的光滑圆形轨道固定在竖直面内。小球A、B质量分别为m、βm(β为待定系数)。A球从左边与圆心等高处由静止开始沿轨道下滑,与静止于轨道最低点的B球相撞,碰撞后A、B球能达到的最大高度均为1/4R,碰撞中无机械能损失。重力加速度为g。
求:(1)待定系数β
(2)第一次碰撞刚结束时小球A、B各自的速度和B球对轨道的压力
(3)小球A、B在轨道最低处第二次碰撞刚结束时各自的速度,并讨论小球A、B在轨道最低处第n次碰撞刚结束时各自的速度
(12分)如右图,半径为R的光滑圆形轨道固定在竖直面内。小球A、B质量分别为m、βm(β为待定系数)。A球从左边与圆心等高处由静止开始沿轨道下滑,与静止于轨道最低点的B球相撞,碰撞后A、B球能达到的最大高度均为1/4R,碰撞中无机械能损失。重力加速度为g。
求:(1)待定系数β
(2)第一次碰撞刚结束时小球A、B各自的速度和B球对轨道的压力
(3)小球A、B在轨道最低处第二次碰撞刚结束时各自的速度,并讨论小球A、B在轨道最低处第n次碰撞刚结束时各自的速度
(12分)如右图,半径为R的光滑圆形轨道固定在竖直面内。小球A、B质量分别为m、βm(β为待定系数)。A球从左边与圆心等高处由静止开始沿轨道下滑,与静止于轨道最低点的B球相撞,碰撞后A、B球能达到的最大高度均为1/4R,碰撞中无机械能损失。重力加速度为g。
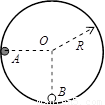
求:(1)待定系数β
(2)第一次碰撞刚结束时小球A、B各自的速度和B球对轨道的压力
(3)小球A、B在轨道最低处第二次碰撞刚结束时各自的速度,并讨论小球A、B在轨道最低处第n次碰撞刚结束时各自的速度
如右图,半径为R的光滑圆形轨道固定在竖直面内。小球A、B质量分别为m、βm(β为待定系数)。A球从左边与圆心等高处由静止开始沿轨道下滑,与静止于轨道最低点的B球相撞,碰撞后A、B球能达到的最大高度均为1/4R,碰撞中无机械能损失。重力加速度为g。

求:(1)待定系数β
(2)第一次碰撞刚结束时小球A、B各自的速度和B球对轨道的压力
(3)小球A、B在轨道最低处第二次碰撞刚结束时各自的速度,并讨论小球A、B在轨道最低处第n次碰撞刚结束时各自的速度

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com