
题目列表(包括答案和解析)
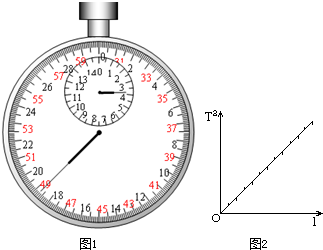
 某同学在做“利用单摆测重力加速度”的实验中,先测得摆线长为59.65cm,然后用秒表记录了单摆振动50次所用的时间为78.5s.则:
某同学在做“利用单摆测重力加速度”的实验中,先测得摆线长为59.65cm,然后用秒表记录了单摆振动50次所用的时间为78.5s.则:| 4π2 |
| K |
| 4π2 |
| K |
| 4π2 |
| K |
| 4π2 |
| K |
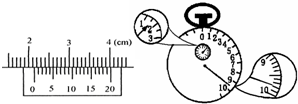 ①某同学在做“利用单摆测重力加速度“实验中先测得摆线长为97.44cm,球直径由如图游标卡尺测得.然后用秒表记录了单摆振动50次所用的时间如图所示,则:小球直径为
①某同学在做“利用单摆测重力加速度“实验中先测得摆线长为97.44cm,球直径由如图游标卡尺测得.然后用秒表记录了单摆振动50次所用的时间如图所示,则:小球直径为| La |
| Lb |
| 4 |
| 9 |
| 4 |
| 9 |


| 4π2 |
| k |
| 4π2 |
| k |
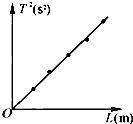 某同学在做“利用单摆测重力加速度“实验:
某同学在做“利用单摆测重力加速度“实验:| 4π2 |
| k |
| 4π2 |
| k |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com