
题目列表(包括答案和解析)
 如图所示,在空间有一坐标系xOy,直线OP与轴正方向的夹角为30°,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP上方区域I中磁场的磁感应强度为B.一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成30°角的方向垂直磁场进入区域I,质子先后通过强磁场区域I和II后,恰好垂直打在x轴上的Q点(图中未画出),则 ( )
如图所示,在空间有一坐标系xOy,直线OP与轴正方向的夹角为30°,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP上方区域I中磁场的磁感应强度为B.一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成30°角的方向垂直磁场进入区域I,质子先后通过强磁场区域I和II后,恰好垂直打在x轴上的Q点(图中未画出),则 ( )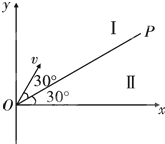 如图所示,在空间有一坐标系xoy,直线OP与x轴正方向的夹角为30°,第一象限内有两个方向都垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ,直线OP是他们的边界,OP上方区域Ⅰ中磁场的磁感应强度为B.一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成30°角的方向垂直磁场进入区域Ⅰ,质子先后通过磁场区域Ⅰ和Ⅱ后,恰好垂直打在x轴上的Q点(图中未画出),则( )
如图所示,在空间有一坐标系xoy,直线OP与x轴正方向的夹角为30°,第一象限内有两个方向都垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ,直线OP是他们的边界,OP上方区域Ⅰ中磁场的磁感应强度为B.一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成30°角的方向垂直磁场进入区域Ⅰ,质子先后通过磁场区域Ⅰ和Ⅱ后,恰好垂直打在x轴上的Q点(图中未画出),则( )A、粒子在区域Ⅰ中运动的时间为
| ||
B、粒子在区域Ⅰ中运动的时间为
| ||
C、粒子在区域Ⅱ中运动的时间为
| ||
D、粒子在区域Ⅱ中运动的时间为
|
如图所示,在空间有一坐标系xoy,直线OP与x轴正方向的夹角为![]() ,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP是它们的边界,OP上方区域I中磁场的磁感应强度为B。一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成
,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP是它们的边界,OP上方区域I中磁场的磁感应强度为B。一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成![]() 角的方向垂直磁场进入区域I,质子先后通过磁场区域I和II后,恰好垂直打在x轴上的Q点(图中未画出),试求:
角的方向垂直磁场进入区域I,质子先后通过磁场区域I和II后,恰好垂直打在x轴上的Q点(图中未画出),试求:
(1)区域II中磁场的磁感应强度大小;
(2)Q点的坐标。

如图所示,在空间有一坐标系xoy,直线OP与x轴正方向的夹角为,第一象限内有两个方向都垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ,直线OP是他们的边界,OP上方区域Ⅰ中磁场的磁感应强度为B。一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成
角的方向垂直磁场进入区域Ⅰ,质子先后通过磁场区域Ⅰ和Ⅱ后,恰好垂直打在x轴上的Q点(图中未画出),则: ( )
A.粒子在第一象限中运动的时间为![]()
B.粒子在第一象限中运动的时间为![]()
C.Q点的横坐标为![]()
![]() D.Q点的横坐标为
D.Q点的横坐标为![]()
如图所示,在空间有一坐标系xOy,其第一象限内充满着两个匀强磁场区域Ⅰ和Ⅱ,直线OP是它们的边界.区域Ⅰ中的磁感应强度为B,方向垂直于纸面向外;区域Ⅱ中的磁感应强度为2B,方向垂直于纸面向内,边界上的P点坐标为(4L,3L).一质量为m、电荷量为q的带正电粒子从P点平行于y轴负方向射入区域Ⅰ,经过一段时间后,粒子恰好经过原点O.忽略粒子重力,已知sin37°=0.6,cos37°=0.8,求:
(1)粒子从P点运动到O点的时间至少为多少?
(2)粒子的速度大小可能是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com