
题目列表(包括答案和解析)
 如图1示,箱子A连同固定在箱子底部的竖直杆的总质量为M=10kg.箱子内部高度H=3.75m,杆长h=2.5m,另有一质量为m=2kg的小铁环B套在杆上,从杆的底部以v0=10m/s的初速度开始向上运动,铁环B刚好能到达箱顶,不计空气阻力,g取10m/s2.求:
如图1示,箱子A连同固定在箱子底部的竖直杆的总质量为M=10kg.箱子内部高度H=3.75m,杆长h=2.5m,另有一质量为m=2kg的小铁环B套在杆上,从杆的底部以v0=10m/s的初速度开始向上运动,铁环B刚好能到达箱顶,不计空气阻力,g取10m/s2.求:
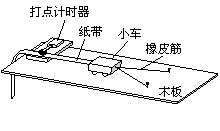
“探究动能定理”的实验装置如图所示,当小车在两条橡皮筋作用下弹出时,橡皮筋对小车做的功记为W0。当用4条、6条、8条……完全相同的橡皮筋并在一起进行第2次、第3次、第4次……实验时,橡皮筋对小车做的功记为2W0、3W0、4W0……,每次实验中由静止弹出的小车获得的最大速度可由打点计时器所打的纸带测出。关于该实验,下列说法正确的是
A.某同学在一次实验中,得到一条记录纸带。纸带上打出的点,两端密、中间疏。出现这种情况的原因,可能是没有使木板倾斜或倾角太小。
B.当小车速度达到最大时,橡皮筋处于伸长状态,小车在两个铁钉的连线处
C.应选择纸带上点距均匀的一段计算小车的最大速度
D.应选择纸带上第一点到最后一点的一段计算小车的最大速度。
(2)某兴趣小组在做“探究做功和物体速度变化关系”的实验前,提出了以下几种猜想:①W∝v,②W∝v2,③W∝![]() 。他们的实验装置如图甲所示,PQ为一块倾斜放置的木板,在Q处固定一个速度传感器(用来测量物体每次通过Q点的速度)。在刚开始实验时,有位同学提出,不需要测出物体质量,只要测出物体初始位置到速度传感器的距离和读出速度传感器的读数就行了,大家经过讨论采纳了该同学的建议。
。他们的实验装置如图甲所示,PQ为一块倾斜放置的木板,在Q处固定一个速度传感器(用来测量物体每次通过Q点的速度)。在刚开始实验时,有位同学提出,不需要测出物体质量,只要测出物体初始位置到速度传感器的距离和读出速度传感器的读数就行了,大家经过讨论采纳了该同学的建议。
①请你简要说明为什么不需要测出物体的质量?
②让小球分别从不同高度无初速释放,测出物体初始位置到速度传感器的距离L1、L2、L3、L4……,读出小球每次通过Q点的速度v1、v2、v3、v4、……,并绘制了如图乙所示的L-v图象。若为了更直观地看出L和v的变化关系,他们下一步应怎么做?


| m | a |
| m | a |
| m | b |
| m | a |
| m | a |
| m | b |
| m | a |
| m | b |
| m | a |
| m | b |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com