
题目列表(包括答案和解析)
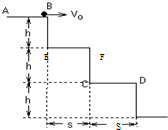 (2007?上海模拟)如图所示,三个台阶每个台阶高h=0.225米,宽s=0.3米.小球在平台AB上以初速度v0水平向右滑出,要使小球正好落在第2个平台CD上,不计空气阻力,求初速v0范围.某同学计算如下:(g取10m/s2)
(2007?上海模拟)如图所示,三个台阶每个台阶高h=0.225米,宽s=0.3米.小球在平台AB上以初速度v0水平向右滑出,要使小球正好落在第2个平台CD上,不计空气阻力,求初速v0范围.某同学计算如下:(g取10m/s2)| 1 |
| 2 |
|
|
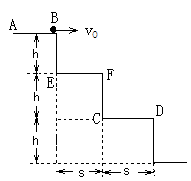
如图所示, 三个台阶每个台阶高 h=0.225 米,宽s=0.3米。小球在平台AB上以初速度v0水平向右滑出,要使小球正好落在第2个平台CD上,不计空气阻力,求初速v0范围。某同学计算如下:(g取10m/s2)
根据平抛规律 2h=gt2/2 ;
到达D点小球的初速 vD =2s/t=2×0.3/0.3=2m/s
到达C点小球的初速 vC =s/t=0.3/0.3=1m/s
所以落到台阶CD小球的初速范围是 1m/s < v0 < 2m/s
以上求解过程是否有问题,若有,指出问题所在,并给出正确的解答。
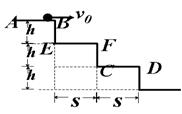
(10分) 如图所示,三个台阶每个台阶高h=0.225m,宽s=0.3m。小球在平台AB上以初速度v0水平向右滑出,要使小球正好落在第2个平台CD上,不计空气阻力,求初速v0范围。
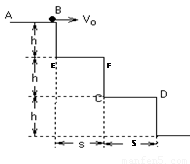
某同学计算如下:(g取10m/s2)根据平抛规律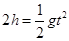 ,
,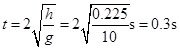
到达D点小球的初速 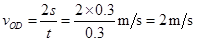
到达C点小球的初速 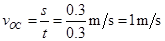

所以落到台阶CD小球的初速范围是 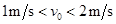
以上求解过程是否有问题,若有,指出问题所在,并给出正确的解答。
 gt2;t=2
gt2;t=2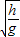 =2
=2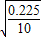 =0.3秒
=0.3秒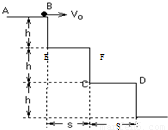
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com