练习册

  • 练习册
  • 试题
    13．[解析](1)设此时盒子的运动周期为T0.因为在最高点时盒子与小球之间刚好无作用力.因此小球仅受重力作用．根据牛顿运动定律得: 解之得: (2)设此时盒子的运动周期为T.则此时小球的向心加速度为: 由第一问知: 且 由上述三式知: 设小球受盒子右侧面的作用力为F.受上侧面的作用力为N.根据牛顿运动定律知: 在水平方向上: 即: 在竖直方向上: 即: 因为F为正值.N为负值.所以小球对盒子的右侧面和下侧面有作用力． 【查看更多】

     

    题目列表(包括答案和解析)

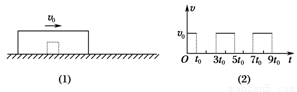
    一个物体静置于光滑水平面上，外面扣一质量为M的盒子，如图(1)所示．现给盒子一初速度v0，此后，盒子运动的v－t图象呈周期性变化，如图(2)所示．请据此求盒内物体的质量．

     

    【解析】：设物体的质量为m，t0时刻受盒子碰撞获得速度v，根据动量守恒定律

    Mv0＝mv，①

    3t0时刻物体与盒子右壁碰撞使盒子速度又变为v0，说明碰撞是弹性碰撞

    mv＝mv2，②

    联立①②解得m＝M.

    (也可通过图象分析得出v0＝v，结合动量守恒，得出正确结果)

     

     

    查看答案和解析>>

    一个物体静置于光滑水平面上，外面扣一质量为M的盒子，如图(1)所示．现给盒子一初速度v0，此后，盒子运动的v－t图象呈周期性变化，如图(2)所示．请据此求盒内物体的质量．

     

    【解析】：设物体的质量为m，t0时刻受盒子碰撞获得速度v，根据动量守恒定律

    Mv0＝mv，①

    3t0时刻物体与盒子右壁碰撞使盒子速度又变为v0，说明碰撞是弹性碰撞

    mv＝mv2，②

    联立①②解得m＝M.

    (也可通过图象分析得出v0＝v，结合动量守恒，得出正确结果)

     

     

    查看答案和解析>>


    同步练习册答案