
题目列表(包括答案和解析)
如下左图所示的电路中,电源的电动势为100V,内阻不计,电阻R=100Ω,且阻值不随温度变化,一个灯泡L两端的电压与流过的电流关系如下表所示,保持环境温度20 ℃不变。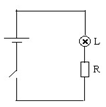
| 电流(A) | 0.20 | 0.37 | 0.50 | 0.60 | 0.68 | 0.75 | 0.78 | 0.79 | 0.80 | 0.80 |
| 电压(V) | 10.0 | 20.0 | 30.0 | 40.0 | 50.0 | 60.0 | 70.0 | 80.0 | 90.0 | 100.0 |

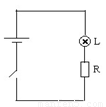
如下左图所示的电路中,电源的电动势为100V,内阻不计,电阻R=100Ω,且阻值不随温度变化,一个灯泡L两端的电压与流过的电流关系如下表所示,保持环境温度20 ℃不变。
|
电流(A) |
0.20 |
0.37 |
0.50 |
0.60 |
0.68 |
0.75 |
0.78 |
0.79 |
0.80 |
0.80 |
|
电压(V) |
10.0 |
20.0 |
30.0 |
40.0 |
50.0 |
60.0 |
70.0 |
80.0 |
90.0 |
100.0 |
(1)试在下面右图给出的坐标中作出灯泡L的伏安特性曲线。
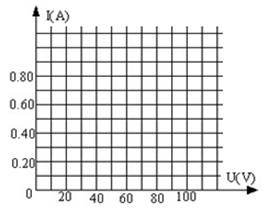
(2)当电键闭合时,灯泡的实际功率为 。简单说明解析过程:
(3)设每秒钟灯泡L向外散射热与周围温度每差1 ℃时为0.24J,则此时灯泡L的温度为多少?
答:
如图2所示,两根平行的金属导轨,固定在同一水平面上,磁感应强度B=0.05 T的匀强磁场与导轨所在平面垂直(图中未画出),导轨的电阻很小,可忽略不计.导轨间的距离l=0.20 m.两根质量均为m=0.10 kg的平行金属杆甲、乙可在导轨上无摩擦地滑动,滑动过程中与导轨保持垂直,每根金属杆的电阻均为R=0.50 Ω.在t=0时刻,两杆都处于静止状态.现有一与导轨平行、大小为0.20 N的恒力F作用于金属杆甲上,使金属杆在导轨上滑动.经过t=5.0 s,金属杆甲的加速度为a=1.37 m/s2.问此时两金属杆的速度各为多少??
图2
【解析】设t=5.0 s时两金属杆甲、乙之间的距离为x,速度分别为v1和v2,经过很短的时间Δt,杆甲移动距离v1Δt,杆乙移动距离v2Δt,回路面积改变ΔS=[(x-v2Δt)+v1Δt]l-lx=(v1-v2)lΔt.由法拉第电磁感应定律知,回路中的感应电动势回路中的电流
对杆甲由牛顿第二定律有F-BlI=ma
由于作用于杆甲和杆乙的安培力总是大小相等、方向相反,所以t=5.0 s时两杆的动量(t=0时为0)等于外力F的冲量Ft=mv1+mv2
联立以上各式解得
代入数据得v1=8.15 m/s,v2=1.85 m/s.
如图2所示,两根平行的金属导轨,固定在同一水平面上,磁感应强度B=0.05 T的匀强磁场与导轨所在平面垂直(图中未画出),导轨的电阻很小,可忽略不计.导轨间的距离l=0.20 m.两根质量均为m=0.10 kg的平行金属杆甲、乙可在导轨上无摩擦地滑动,滑动过程中与导轨保持垂直,每根金属杆的电阻均为R=0.50 Ω.在t=0时刻,两杆都处于静止状态.现有一与导轨平行、大小为0.20 N的恒力F作用于金属杆甲上,使金属杆在导轨上滑动.经过t=5.0 s,金属杆甲的加速度为a=1.37 m/s2.问此时两金属杆的速度各为多少??

图2
【解析】设t=5.0 s时两金属杆甲、乙之间的距离为x,速度分别为v1和v2,经过很短的时间Δt,杆甲移动距离v1Δt,杆乙移动距离v2Δt,回路面积改变ΔS=[(x-v2Δt)+v1Δt]l-lx=(v1-v2)lΔt.由法拉第电磁感应定律知,回路中的感应电动势 回路中的电流
回路中的电流
对杆甲由牛顿第二定律有F-BlI=ma
由于作用于杆甲和杆乙的安培力总是大小相等、方向相反,所以t=5.0 s时两杆的动量(t=0时为0)等于外力F的冲量Ft=mv1+mv2
联立以上各式解得


代入数据得v1=8.15 m/s,v2=1.85 m/s.
已知氢原子基态的电子轨道半径r1=0.53×10-10 m,基态的能级值为E1=-13.6 eV.
(1)求电子在n=1的轨道上运动形成的等效电流.
(2)有一群氢原子处于量子数n=3的激发态,画出能级图,在图上用箭头标明这些氢原子能发出哪几条光谱线.
(3)计算这几条光谱线中最长的波长.
【解析】:(1)电子绕核运动具有周期性,设运转周期为T,由牛顿第二定律和库仑定律有:k=m2r1①
又轨道上任一处,每一周期通过该处的电荷量为e,由电流的定义式得所求等效电流I=②
联立①②式得
I=
=× A
=1.05×10-3 A

(2)由于这群氢原子的自发跃迁辐射,会得到三条光谱线,如右图所示.
(3)三条光谱线中波长最长的光子能量最小,发生跃迁的两个能级的能量差最小,根据氢原子能级的分布规律可知,氢原子一定是从n=3的能级跃迁到n=2的能级
设波长为λ,由h=E3-E2,得
λ=
=m
=6.58×10-7m
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com