如图13-9-12所示，质量为m=2×10^－15 kg、q=－3×10^－10 C的带电粒子，自A点垂直电场线方向进入有界的匀强电场，它从B点飞出时v_B=6×10³ m/s,v_B与E交角120°.已知AB沿电场线方向相距15 cm，不计重力，求：

(1)U_BA的大小；

(2)粒子A到B的时间；

(3)匀强电场的宽度.

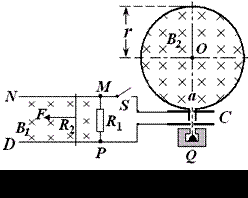
如图所示，光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上，两导轨间距l = 0.2m，电阻R₁ = 0.4Ω，导轨上静止放置一质量m = 0.1kg、电阻R₂  = 0.1Ω的金属杆，导轨电阻忽略不计，整个装置处在磁感应强度B₁ = 0.5T的匀强磁场中，磁场的方向竖直向下，现用一外力F沿水平方向拉杆，使之由静止起做匀加速运动并开始计时，若5s末杆的速度为2.5m/s，求：

（1）5s末时电阻R上消耗的电功率；

（2）5s末时外力F的功率.

（3）若杆最终以8 m/s的速度作匀速运动, 此时闭合电键S，射线源Q释放的粒子经加速电场C加速后从a孔对着圆心O进入半径r = m的固定圆筒中（筒壁上的小孔a只能容一个粒子通过），圆筒内有垂直水平面向下的磁感应强度为B₂的匀强磁场。粒子每次与筒壁发生碰撞均无电荷迁移，也无机械能损失，粒子与圆筒壁碰撞5次后恰又从a孔背离圆心射出，忽略粒子进入加速电场的初速度，若粒子质量= 6.6×10^{－27 kg ,} 电量= 3.2×10^{－19 C,} 则磁感应强度B₂ 多大？若不计碰撞时间，粒子在圆筒内运动的总时间多大？

如图9所示，有一磁感应强度B=9.1×10^－4T的匀强磁场，C、D为垂直于磁场的同一平面内的两点，它们之间的距离l=0.05m，今有一电子在此磁场中运动，它经过C点时的速度v的方向和磁场方向垂直，且与CD间的夹角α=30°，问：

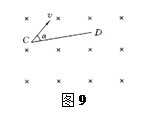（1）电子在C点时所受的洛仑兹力的方向如何?

（2）若此电子在运动中后来又经过了D点，则它的速度v应是多大?

（3）电子从C点到D点所用的时间是多少（电子的质量m=9.1×10^－31kg，电子的电量e=1.6×10^－19C）？

（18分）如图甲所示，在边界MN左侧存在斜方向的匀强电场E₁，在MN的右侧有竖直向上、场强大小为E₂＝0．4N/C的匀强电场，还有垂直纸面向内的匀强磁场B（图甲中未画出）和水平向右的匀强电场E₃（图甲中未画出），B和E₃随时间变化的情况如图乙所示，P₁P₂为距MN边界2．295m的竖直墙壁，现有一带正电微粒质量为4×10^－7kg，电量为1×10^－5C，从左侧电场中距MN边界m的A处无初速释放后，沿直线以1m/s速度垂直MN边界进入右侧场区，设此时刻t＝0， 取g ＝10m/s²。求：

　　　　

（1）MN左侧匀强电场的电场强度E₁（sin37°＝0．6）；

（2）带电微粒在MN右侧场区中运动了1．5s时的速度；

（3）带电微粒在MN右侧场区中运动多长时间与墙壁碰撞？（≈0．19）

如图所示，一根长L＝1.5 m的光滑绝缘细直杆MN，竖直固定在场强为E＝1.0×105 N/C、与水平方向成θ＝30°角的倾斜向上的匀强电场中。杆的下端M固定一个带电小球A，电荷量Q＝+4.5×10－6 C；另一带电小球B穿在杆上可自由滑动，电荷量q＝+1.0×10一6 C，质量m＝1.0×10一2 kg。现将小球B从杆的上端N静止释放，小球B开始运动。（静电力常量k＝9.0×109 N·m2／C2，取g＝l0 m/s2)

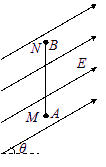
（1）小球B开始运动时的加速度为多大？

（2）小球B的速度最大时，距M端的高度h1为多大？

（3）小球B从N端运动到距M端的高度h2＝0.6l m时，速度为v＝1.0 m/s，求此过程中小球B的电势能改变了多少？