
题目列表(包括答案和解析)
 如图所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子.在放射源右侧有一很薄的挡板,垂直于x轴放置,挡板与xoy平面交线的两端M、N正好与原点O构成等边三角形,O′为挡板与x轴的交点.在整个空间中,有垂直于xoy平面向外的匀强磁场(图中未画出),带电粒子在磁场中沿顺时针方向做匀速圆周运动.已知带电粒子的质量为m,带电荷量大小为q,速度大小为υ,MN的长度为L.(不计带电粒子的重力及粒子间的相互作用)
如图所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子.在放射源右侧有一很薄的挡板,垂直于x轴放置,挡板与xoy平面交线的两端M、N正好与原点O构成等边三角形,O′为挡板与x轴的交点.在整个空间中,有垂直于xoy平面向外的匀强磁场(图中未画出),带电粒子在磁场中沿顺时针方向做匀速圆周运动.已知带电粒子的质量为m,带电荷量大小为q,速度大小为υ,MN的长度为L.(不计带电粒子的重力及粒子间的相互作用)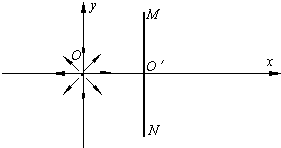 如图所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子.在放射源右边有一很薄的挡板,挡板与xoy平面交线的两端M、N与原点O正好构成等腰直角三角形.已知带电粒子的质量为m,带电量为q,速度为υ,MN的长度为L.(不计带电粒子的重力)
如图所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子.在放射源右边有一很薄的挡板,挡板与xoy平面交线的两端M、N与原点O正好构成等腰直角三角形.已知带电粒子的质量为m,带电量为q,速度为υ,MN的长度为L.(不计带电粒子的重力)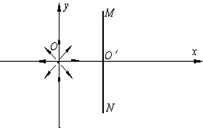 如图所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子.在放射源右边有一很薄的挡板,挡板与xoy平面交线的两端M、N与原点O正好构成等腰直角三角形.已知带电粒子的质量为m,带电量为q,速度为υ,MN的长度为L.若在y轴右侧加一平行于x轴的匀强电场,要使y轴右侧所有运动的粒子都能打到挡板MN上,则电场强度E0的最小值为
如图所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子.在放射源右边有一很薄的挡板,挡板与xoy平面交线的两端M、N与原点O正好构成等腰直角三角形.已知带电粒子的质量为m,带电量为q,速度为υ,MN的长度为L.若在y轴右侧加一平行于x轴的匀强电场,要使y轴右侧所有运动的粒子都能打到挡板MN上,则电场强度E0的最小值为如图所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子。在放射源右边有一很薄的挡板,挡板与xOy平面交线的两端M、N与原点O正好构成等腰直角三角形。已知带电粒子的质量为m,带电量为q,速度为v,MN的长度为L。
(1)若在y轴右侧加一平行于x轴的匀强电场,要使y轴右侧所有运动的粒子都能打到挡板MN上,则电场强度![]() 的最小值为多大?在电场强度为
的最小值为多大?在电场强度为![]() 时,打到板上的粒子动能为多大?
时,打到板上的粒子动能为多大?
(2)若在整个空间加一方向垂直纸面向里的匀强磁场,要使板右侧的MN连线上都有粒子打到,磁场的磁感应强度不能超过多少(用m、v、q、L表示)?若满足此条件,放射源O向外发射出的所有带电粒子中有几分之几能打在板的左边?
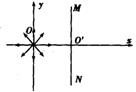
如图所示,在直角坐标系的原点O 处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子。在放射源右侧有一很薄的挡板,垂直于x 轴放置,挡板与xoy 平面交线的两端M、N 正好与原点O 构成等边三角形,O′ 为挡板与x 轴的交点。在整个空间中,有垂直于xoy 平面向外的匀强磁场(图中未画出),带电粒子在磁场中沿顺时针方向做匀速圆周运动。已知带电粒子的质量为m,带电荷量大小为q,速度大小为υ,MN 的长度为L。(不计带电粒子的重力及粒子间的相互作用)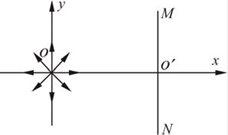
(1)确定带电粒子的电性;
(2)要使带电粒子不打在挡板上,求磁感应强度的最小值;
(3)要使MN 的右侧都有粒子打到,求磁感应强度的最大值。(计算过程中,要求画出各临界状态的轨迹图)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com